TMBR: October 2025

Prev: September 2025

This Month in Beaver Research

Next: November 2025

This edition of TMBR is in progress and has not yet been released. Please add any notes you think may be relevant (including in the form a of a TODO with a link to any relevant Discord discussion).

TODO: BB(3x3) month

TODO: BB(2x5) month next month (?)

A brave busy beaver confronts the dreaded Antihydra. Copyright Nico Roper.

Misc

@Bricks shared a method to measure susceptibility to block-analysis¹, which resulted in the following spreadsheet of machines which should be easiest to solve using Block-Analysis.

@coda shared a mechanical implementation of a Turing Machine¹, Antihydra.

Wily Coyote, a BB(3,3) holdout

Blog Posts

• 22 Oct 2025. Ben Brubaker. Why Busy Beaver Hunters Fear the Antihydra.

Champions

• BB(4,3):
  • Polygon analysed the remaining potential champions discovered by Pavel Kropitz in May 2024, discovering that 1RB1RD1LC_2LB1RB1LC_1RZ1LA1LD_0RB2RA2RD (bbch) is the new BB(4,3) champion with a score of over $10{\uparrow }^{4}4$.

Holdouts

BB(6) Holdouts count decrease overtime.

BB Holdout Reduction by Domain

Domain	New Holdout Count	Previous Holdout Count	Holdout Reduction	% Reduction
BB(6)	1618	1691	73	4.3%
BB(7)	20,405,295	22,801,601	2,396,306	10.5%
BB(4,3)	9,401,447	460,916,384	451,514,937	98.0%
BB(3,4)	15,136,283	434,787,751	419,651,468	96.6%
BB(2,6)	870,085	873,469	3384	0.4%

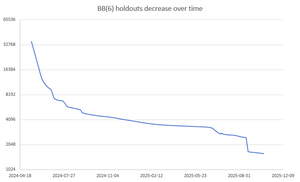
• BB(6):
  • @mxdys shared a new holdouts list on October 20th, consisting of 1618 machines up to equivalence, or 3067 individual machines. This means 73 newly solved machines, a 4% reduction.
  • @Bricks shared a machine which they thought could be susceptible to block-analysis based on a method they call Subtape Saturation Heuristic. Shawn Ligocki's analysis, simulated by @Bricks showed the machine to halt with a sigma score of 4,419,340,317.
  • Analysis by Racheline showed a machine to be non-halting.
  • mxdys decided a machine from the 50 Random Holdouts introduced back in August, making 10/50 solved.
  • Peacemaker II mentioned a machine which visits only 24 cells after a million steps. mxdys proved the machine nonhalting.
• BB(7):
  • Andrew Ducharme has continued reducing the number of holdouts with Stage 4 of Phase 2. Afterwards, Terry Ligocki ran Stage 5 of Phase 2. Initially, in the beginning of the month there were 22,801,601 holdouts, and 20,405,295 holdouts remain. (10.51% reduction)
• BB(4,3):
  • Terry Ligocki has begun Phase 2 of holdout reduction, reducing the number of holdouts from 460,916,384 to 9,401,447. (97.96% reduction)
• BB(3,4):
  • XnoobSpeakable and Lúkos are running filters in the domain under Phase 2, reducing the holdout count from 434,787,751 to 15,136,283. (96.6% reduction)
• BB(2,5):
  • Peacemaker II gave an informal proof of a machine never halting, making the informal holdout count 64.
• BB(2,6):
  • Andrew Ducharme has completed Stage 3 of Phase 2, reducing the number of holdouts from 873,469 to 870,085. (0.39% reduction)

Theory

Piecewise Affine Functions (PAF) were explored as a generalization of the BMO1 rules:

• @Bard proved that 3 dimension PAF are Turing complete: [1]
• @star proved that 2 dimension PAF are Turing complete: [2]
• Shawn Ligocki wrote up a proof sketch that 2-region PAF are Turing complete: [3]
• It was discovered that Amir Ben-Amram had already proven that 2-dim and 2-region PAF were Turing complete in 2015.
• BMO1 is a 2-dim, 2-region PAF so this provides some sense for the difficulty of the problem.

Deciders

• Inductive deciders
  • -d rewrote quick_sim.py in C++, achieving a 6-10x faster runtime¹².
  • Katelyn Douchette is working on an automated inductive decider^12. (see inductive proofs)