Antihydra

Unsolved problem:

Does Antihydra run forever?

1RB1RA_0LC1LE_1LD1LC_1LA0LB_1LF1RE_---0RA (bbch), called Antihydra, is a BB(6) Cryptid. Its pseudo-random behaviour was first reported on Discord by mxdys on 28 June 2024, and Racheline discovered the high-level rules soon after. It was named after the 2-state, 5-symbol Turing machine called Hydra for sharing many similarities to it.

Antihydra is known to not generate Sturmian words (Corollary 4).

Artistic depiction of Antihydra by Jadeix

0 1 A 1RB 1RA B 0LC 1LE C 1LD 1LC D 1LA 0LB E 1LF 1RE F --- 0RA The transition table of Antihydra.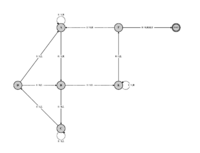

State diagram of Antihydra

A community trophy - to be awarded to the first person or group who solves the Antihydra problem

Analysis

Let $A(a,b):=0^{\mathrm{\infty }}{1}^{a}01^b\text{E}\text{<mo>></mo>}{0}^{\mathrm{\infty }}$. Then, $$\begin{array}{lll}A(a,2b)& \stackrel{2a+3b^2+12b+11}{\to }& A(a+2,3b+2),\\ A(0,2b+1)& \stackrel{3b^2+9b-1}{\to }& 0^{\mathrm{\infty }}\text{<mo><</mo>}\text{F}1101^{3b}{0}^{\mathrm{\infty }},\\ A(a+1,2b+1)& \stackrel{3b^2+12b+5}{\to }& A(a,3b+3).\end{array}$$

Proof

Consider the partial configuration $P(m,n):=01^m\text{E}\text{<mo>></mo>}01^n{0}^{\mathrm{\infty }}$. The configuration after two steps is $01^{m-1}0\text{A}\text{<mo>></mo>}{1}^{n+1}{0}^{\mathrm{\infty }}$. We note the following shift rule: $$\begin{array}{c}\text{A}\text{<mo>></mo>}{1}^s\stackrel{s}{\to }{1}^s\text{A}\text{<mo>></mo>}\end{array}$$ As a result, we get $01^{m-1}01^{n+1}\text{A}\text{<mo>></mo>}{0}^{\mathrm{\infty }}$ after $n+1$ steps. Advancing two steps produces $01^{m-1}01^{n+2}\text{<mo><</mo>}\text{C}{0}^{\mathrm{\infty }}$. A second shift rule is useful here: $$\begin{array}{c}{1}^s\text{<mo><</mo>}\text{C}\stackrel{s}{\to }\text{<mo><</mo>}\text{C}{1}^s\end{array}$$ This allows us to reach $01^{m-1}0\text{<mo><</mo>}\text{C}{1}^{n+2}{0}^{\mathrm{\infty }}$ in $n+2$ steps. Moving five more steps gets us to $01^{m-2}\text{E}\text{<mo>></mo>}01^{n+3}{0}^{\mathrm{\infty }}$, which is the same configuration as $P(m-2,n+3)$. Accounting for the head movement creates the condition that $m\ge 4$. In summary: $$\begin{array}{c}P(m,n)\stackrel{2n+12}{\to }P(m-2,n+3)\text{ if }m\ge 4.\end{array}$$ With $A(a,b)$ we have $P(b,0)$. As a result, we can apply this rule $\lfloor \frac{1}{2}b\rfloor -1$ times (assuming $b\ge 4$), which creates two possible scenarios:

1. If $b\equiv 0(\mathrm{mod}2)$, then in $\sum _{i=0}^{(b/2)-2}(2\times 3i+12)=\frac{3}{4}{b}^2+\frac{3}{2}b-6$ steps we arrive at $P(2,\frac{3}{2}b-3)$. The matching complete configuration is $0^{\mathrm{\infty }}{1}^{a}011\text{E}\text{<mo>></mo>}01^{(3b)/2-3}{0}^{\mathrm{\infty }}$. After $3b+4$ steps this is $0^{\mathrm{\infty }}{1}^a\text{<mo><</mo>}\text{C}001^{(3b)/2}{0}^{\mathrm{\infty }}$, which then leads to $0^{\mathrm{\infty }}\text{<mo><</mo>}\text{C}{1}^{a}001^{(3b)/2}{0}^{\mathrm{\infty }}$ in $a$ steps. After five more steps, we reach $0^{\mathrm{\infty }}1\text{E}\text{<mo>></mo>}{1}^{a+2}001^{(3b)/2}{0}^{\mathrm{\infty }}$, from which another shift rule must be applied:$$\begin{array}{c}\text{E}\text{<mo>></mo>}{1}^s\stackrel{s}{\to }{1}^s\text{E}\text{<mo>></mo>}\end{array}$$Doing so allows us to get the configuration $0^{\mathrm{\infty }}{1}^{a+3}\text{E}\text{<mo>></mo>}001^{(3b)/2}{0}^{\mathrm{\infty }}$ in $a+2$ steps. In six steps we have $0^{\mathrm{\infty }}{1}^{a+2}011\text{E}\text{<mo>></mo>}{1}^{(3b)/2}{0}^{\mathrm{\infty }}$, so we use the shift rule again, ending at $0^{\mathrm{\infty }}{1}^{a+2}01^{(3b)/2+2}\text{E}\text{<mo>></mo>}{0}^{\mathrm{\infty }}$, equal to $A(a+2,\frac{3}{2}b+2)$, $\frac{3}{2}b$ steps later. This gives a total of $2a+\frac{3}{4}{b}^2+6b+11$ steps.
2. If $b\equiv 1(\mathrm{mod}2)$, then in $\frac{3}{4}{b}^2-\frac{27}{4}$ steps we arrive at $P(3,\frac{3b-9}{2})$. The matching complete configuration is $0^{\mathrm{\infty }}{1}^{a}0111\text{E}\text{<mo>></mo>}01^{(3b-9)/2}{0}^{\mathrm{\infty }}$. After $3b+2$ steps this becomes $0^{\mathrm{\infty }}{1}^a\text{<mo><</mo>}\text{F}1101^{(3b-3)/2}{0}^{\mathrm{\infty }}$. If $a=0$ then we have reached the undefined F0 transition with a total of $\frac{3}{4}{b}^2+3b-\frac{19}{4}$ steps. Otherwise, continuing for six steps gives us $0^{\mathrm{\infty }}{1}^{a-1}0111\text{E}\text{<mo>></mo>}{1}^{(3b-3)/2}{0}^{\mathrm{\infty }}$. We conclude with the configuration $0^{\mathrm{\infty }}{1}^{a-1}01^{(3b+3)/2}\text{E}\text{<mo>></mo>}{0}^{\mathrm{\infty }}$, equal to $A(a-1,\frac{3b+3}{2})$, in $\frac{3b-3}{2}$ steps. This gives a total of $\frac{3}{4}{b}^2+\frac{9}{2}b-\frac{1}{4}$ steps.

The information above can be summarized as $$A(a,b)\to \{\begin{array}{ll}A(a+2,\frac{3}{2}b+2)& \text{if }b\ge 2,b\equiv 0(\mathrm{mod}2);\\ 0^{\mathrm{\infty }}\text{<mo><</mo>}\text{F}1101^{(3b-3)/2}{0}^{\mathrm{\infty }}& \text{if }b\ge 3,b\equiv 1(\mathrm{mod}2),\text{ and }a=0;\\ A(a-1,\frac{3b+3}{2})& \text{if }b\ge 3,b\equiv 1(\mathrm{mod}2),\text{ and }a>0.\end{array}$$ Substituting $b\leftarrow 2b$ for the first case and $b\leftarrow 2b+1$ for the other two yields the final result.

In effect, the halting problem for Antihydra is about whether repeatedly applying the function $f(n)=\lfloor \frac{3n}{2}\rfloor +2$ will at some point produce more odd values of $n$ than twice the number of even values.

These rules can be modified to use the function $H(n)=\lfloor \frac{3n}{2}\rfloor$, or the Hydra function, which strengthens Antihydra's similarities to Hydra.

Trajectory

Path of parity of repeated applications of Hydra map for Antihydra.

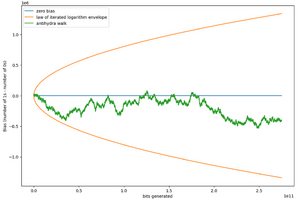
Starting from a blank tape, Antihydra reaches $A(0,4)$ in 11 steps and then the rules are repeatedly applied. So far, Antihydra has been simulated to $2^{38}$ rule steps, at which point $a$ exceeds $2^{37}$. Here are the first few: $$\begin{array}{c}A(0,4)\stackrel{47}{\to }A(2,8)\stackrel{111}{\to }A(4,14)\stackrel{250}{\to }A(6,23)\stackrel{500}{\to }A(5,36)\stackrel{1209}{\to }A(7,56)\stackrel{2713}{\to }A(9,86)\to \cdots \end{array}$$ The trajectory of $a$ values resembles a random walk in which the walker can only move in step sizes +2 or -1 with equal probability, starting at position 0. If $P(n)$ is the probability that the walker will reach position -1 from position $n$, then it can be seen that $P(n)=\frac{1}{2}P(n-1)+\frac{1}{2}P(n+2)$. Solutions to this recurrence relation come in the form $P(n)=c_0{\left(\frac{\sqrt{5}-1}{2}\right)}^n+c_1+c_2{(-\frac{1+\sqrt{5}}{2})}^n$, which after applying the appropriate boundary conditions reduces to $P(n)={\left(\frac{\sqrt{5}-1}{2}\right)}^{n+1}$. This means that if the walker were to get to the position of the current $a$ value, then the probability of it ever reaching position -1 is less than ${\left(\frac{\sqrt{5}-1}{2}\right)}^{2^{37}}\approx 2.884\times 10^{-28723042565}$. This combined with the fact that the expected position of the walker after $k$ steps is $\frac{1}{2}k$ strongly suggests Antihydra probviously runs indefinitely.

Code

The following Python program implements the abstracted behavior of the Antihydra. Proving whether it halts or not would also solve the Antihydra problem:

# Current value of the iterated Hydra function starting with initial value 8 (the values do not overflow)
h = 8
# (Collatz-like) condition counter that keeps track of how many odd and even numbers have been encountered
c = 0
# If c equals -1 there have been (strictly) more than twice as many odd as even numbers and the program halts
while c != -1:
    # If h is even, add 2 to c so even numbers count twice
    if h % 2 == 0:
        c += 2
    else:
        c -= 1
    # Add the current hydra value divided by two (integer division, rounding down) to itself (Hydra function)
    # Note that integer division by 2 is equivalent to one bit shift to the right (h >> 1)
    h += h//2

The variable values of this iteration have been put into the On-Line Encyclopedia of Integer Sequences (OEIS):

• Hydra function values with Antihydra's starting value 8: https://oeis.org/A386792
• Antihydra's condition values: https://oeis.org/A385902

Fast Hydra/Antihydra simulation code by Greg Kuperberg (who said it could be made faster using FLINT):

# Python script to demonstrate almost linear time hydra simulation
# using fast multiplication. 
# by Greg Kuperberg

import time
from gmpy2 import mpz,bit_mask

# Straight computation of t steps of hydra
def simple(n,t):
    for s in range(t): n += n>>1
    return n

# Accelerated computation of 2**e steps of hydra
def hydra(n,e):
    if e < 9: return simple(n,1<<e)
    t = 1<<(e-1)
    (p3t,m) = (mpz(3)**t,bit_mask(t))
    n = p3t*(n>>t) + hydra(n&m,e-1)
    return p3t*(n>>t) + hydra(n&m,e-1)

def elapsed():
    (last,elapsed.mark) = (elapsed.mark,time.process_time())
    return elapsed.mark-last
elapsed.mark = 0

(n,e) = (mpz(3),25)

elapsed()
print('hydra:  steps=%d hash=%016x time=%.6fs'
    % (1<<e,hash(hydra(n,e)),elapsed()))

# Quadratic time algorithm for comparison
# print('simple: steps=%d hash=%016x time=%.6fs'
#     % (1<<e,hash(simple(n,1<<e)),elapsed()))