BB(6)

The 6-state, 2-symbol Busy Beaver problem, BB(6), refers to the unsolved 6^th value of the Busy Beaver function. With the discovery of the Cryptid machine Antihydra in June 2024, we now know that we must solve a Collatz-like problem in order to solve BB(6) and thus BB(6) is Hard.

The current BB(6) champion 1RB1RA_1RC1RZ_1LD0RF_1RA0LE_0LD1RC_1RA0RE (bbch) was discovered by mxdys in June 2025, proving the lower bound:

$$S(6)>\Sigma (6)>2\uparrow \uparrow \uparrow 5$$

Techniques

Simulating tetrational machines, such as the former champion 1RB0LD_1RC0RF_1LC1LA_0LE1RZ_1LF0RB_0RC0RE (bbch), requires accelerated simulation that can handle Collatz Level 2 inductive rules. In other words, it requires a simulator that can prove the rules:

$${\begin{array}{lcl}C(4k)&\to &{\operatorname {Halt} }{\Big (}{\frac {3^{k+3}-11}{2}}{\Big )}\\C(4k+1)&\to &C{\Big (}{\frac {3^{k+3}-11}{2}}{\Big )}\\C(4k+2)&\to &C{\Big (}{\frac {3^{k+3}-11}{2}}{\Big )}\\C(4k+3)&\to &C{\Big (}{\frac {3^{k+3}+1}{2}}{\Big )}\\\end{array}}$$

and also compute the remainder mod 3 of numbers produced by applying these rules 15 times (which requires some fancy math related to Euler's totient function).

Another technique used to reduce the holdout count is using automatic decider programs, such as Shawn Ligocki's Enumerate.py. The holdouts have been run through this code with the following parameters: python3 Code/Enumerate.py --infile "bb6in/bb6tm{i}.txt" --outfile "bb6out/t{i}.pb" -r --no-steps --exp-linear-rules --exp-meta-linear-rules --max-loops=50_000_000 --block-mult=3 --max-block-size=100 --time=500 --force --save-freq=1 And also with the parameters --block-mult=2 and --block-mult=3

Cryptids

Several Turing machines have been found that are Cryptids, considered so because each of them have a Collatz-like halting problem, a type of problem that is generally difficult to solve. However, probabilistic arguments have allowed all but one of them to be categorized as probviously halting or probviously non-halting.

Probviously non-halting Cryptids:

• 1RB1RA_0LC1LE_1LD1LC_1LA0LB_1LF1RE_---0RA (bbch), Antihydra
• 1RB1RC_1LC1LE_1RA1RD_0RF0RE_1LA0LB_---1RA (bbch), a variant of Hydra and Antihydra
• 1RB1LD_1RC1RE_0LA1LB_0LD1LC_1RF0RA_---0RC (bbch), similar to Antihydra
• 1RB0LD_1RC1RF_1LA0RA_0LA0LE_1LD1LA_0RB--- (bbch), similar to Antihydra
• 1RB0LB_1LC0RE_1LA1LD_0LC---_0RB0RF_1RE1RB (bbch), similar to Antihydra
• 1RB1LA_1LC0RE_1LF1LD_0RB0LA_1RC1RE_---0LD (bbch)

Probviously halting Cryptids:

• 1RB0RD_0RC1RE_1RD0LA_1LE1LC_1RF0LD_---0RA (bbch), Lucy's Moonlight
• 1RB1RA_0RC1RC_1LD0LF_0LE1LE_1RA0LB_---0LC (bbch), a family of 16 related TMs
• 1RB1RE_1LC1LD_---1LA_1LB1LE_0RF0RA_1LD1RF (bbch)
• 1RB0RE_1LC1LD_0RA0LD_1LB0LA_1RF1RA_---1LB (bbch)
• 1RB0LC_0LC0RF_1RD1LC_0RA1LE_---0LD_1LF1LA (bbch)
• 1RB0LC_1LC0RD_1LF1LA_1LB1RE_1RB1LE_---0LE (bbch)
• 1RB---_0RC0RE_1RD1RF_1LE0LB_1RC0LD_1RC1RA (bbch)
• 1RB0LD_1RC1RA_1LD0RB_1LE1LA_1RF0RC_---1RE (bbch)

Although 1RB1LE_0LC0LB_1RD1LC_1RD1RA_1RF0LA_---1RE (bbch) behaves similarly to the probviously halting Cryptids, it is estimated to have a 3/5 chance of becoming a translated cycler and a 2/5 chance of halting.

There are a few machines considered notable for their chaotic behaviour, but which have not been classified as Cryptids due to seemingly lacking a connection to any known open mathematical problems, such as Collatz-like problems.

Potential Cryptids:

• 1RB1RE_1LC0RA_0RD1LB_---1RC_1LF1RE_0LB0LE (bbch)
• 1RB0LD_1LC0RA_1RA1LB_1LA1LE_1RF0LC_---0RE (bbch)
• 1RB0RB_1LC1RE_1LF0LD_1RA1LD_1RC1RB_---1LC (bbch)

Top Halters

Below is a table of the machines with the 10 highest known runtimes. Their sigma scores are expressed using an extension of Knuth's up-arrow notation.

Top Known BB(6) Halters

Standard format	(approximate) Σ
1RB1RA_1RC1RZ_1LD0RF_1RA0LE_0LD1RC_1RA0RE (bbch)	2 ↑↑↑ 5
1RB1LC_1LA1RE_0RD0LA_1RZ1LB_1LD0RF_0RD1RB (bbch)	10 ↑↑ 11010000
1RB0LD_1RC0RF_1LC1LA_0LE1RZ_1LF0RB_0RC0RE (bbch)	10 ↑↑ 15.60465
1RB0LF_1RC1RB_1LD0RA_1LB0LE_1RZ0LC_1LA1LF (bbch)	10 ↑↑ 7.52390
1RB0LF_1RC1RB_1LD0RA_1RF0LE_1RZ0LC_1LA1LF (bbch)	10 ↑↑ 7.52390
1RB0LF_1RC1RB_1LD0RA_1LF0LE_1RZ0LC_1LA1LF (bbch)	10 ↑↑ 7.52390
1RB1RC_1LC1RE_1LD0LB_1RE1LC_1LE0RF_1RZ1RA (bbch)	10 ↑↑ 7.23619
1RB1RA_1LC1LE_1RE0LD_1LC0LF_1RZ0RA_0RA0LB (bbch)	10 ↑↑ 6.96745
1RB0RF_1LC0RA_1RZ0LD_1LE1LD_1RB1RC_0LD0RE (bbch)	10 ↑↑ 5.77573
1RB0LA_1LC1LF_0LD0LC_0LE0LB_1RE0RA_1RZ1LD (bbch)	10 ↑↑ 5.63534

The runtimes are presumed to be about ${\text{score}}^{2}$ which is roughly indistinguishable in tetration notation.

Holdouts

Number of BB(6) holdouts over time

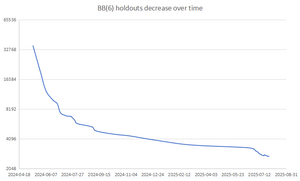
@mxdys's informal holdouts list has 2891 machines up to equivalence as of July 2025.