Fractran

Fractran (originally styled FRACTRAN) is an esoteric Turing complete model of computation invented by John Conway in 1987. In this model a program is simply a finite list of fractions (rational numbers), the program state is an integer. For more details see https://en.wikipedia.org/wiki/FRACTRAN.

Discord user Coda came up with a way to transform any Fractran program into a Turing Machine, see source.

BB_fractran(n) or BBf(n) is the Busy Beaver function for Fractran programs. Holdouts lists by Daniel Yuan: Holdouts lists

Definition

A fractran program is a list of rational numbers $[q_0,q_1,...q_{k-1}]$called rules and a fractran state is an integer $s\in \mathbb{\mathbb{Z}}$. The numerator and denominator of any rational number fraction do not share any prime factors (they are in reduced form). We say that a rule $q_i$ applies to state $s$ if $s\cdot q_i\in \mathbb{\mathbb{Z}}$. If no rule applies, we say that the computation has halted otherwise we apply the first applicable rule at each step. In that case we say $s\to t$ and $t=s\cdot q_i$ and $i=\min \{i:s\cdot q_i\in \mathbb{\mathbb{Z}}\}$. As with Turing machines, we will write $s\stackrel{N}{\to }t$ if $s\to s_1\to \cdots \to s_{N-1}\to t$ (s goes to t after N steps) and $s{\to }^{*}t$ or $s{\to }^{+}t$ if $s\stackrel{N}{\to }t$ for some N≥0 or N≥1 (respectively). We say that a program has runtime N (or halts in N steps) starting in state s if $s\stackrel{N}{\to }t$ and computation halts on t.

Let $\mathrm{\Omega }(n)$ be the total number of prime factors of a positive integer n. In other words, $\mathrm{\Omega }(2^{a_0}{3}^{a_1}\cdots p_n^{a_n})=\sum _{k=0}^n{a}_n$. Then given a rule $\frac{a}{b}$ we say that $\text{size}\left(\frac{a}{b}\right)=\mathrm{\Omega }(a)+\mathrm{\Omega }(b)$. And the size of a fractran program $[q_0,q_1,...q_{k-1}]$ is $k+\sum _{i=0}^{k-1}\text{size}(q_i)$.

BB_fractran(n) or BBf(n) is the maximum runtime starting in state 2 for all halting fractran programs of size n. It is a non-computable function akin to the Busy Beaver Functions since Fractran is Turing Complete.

Vector Representation

Fractran programs are not easy to interpret, in fact it may be completely unclear at first that they can perform any computation at all. One of the key insights is to represent all numbers (states and rules) in their prime factorization form. For example, we can use a vector $[a_0,a_1,\dots ,a_{n-1}]\in {\mathbb{\mathbb{Z}}}^n$ to represent the number $2^{a_0}{3}^{a_1}\cdots p_{n-1}^{a_{n-1}}$.

Let the vector representation (for a sufficiently large n) for a state $a=2^{a_0}{3}^{a_1}\cdots p_{n-1}^{a_{n-1}}$ be $v(a)=[a_0,a_1,\dots ,a_{n-1}]\in {\mathbb{\mathbb{N}}}^n$ and the vector representation for a rule $\frac{a}{b}$ be $v\left(\frac{a}{b}\right)=v(a)-v(b)\in {\mathbb{\mathbb{Z}}}^n$ (Note that this is just an extension of the original definition extended to allow negative $a_i$).

Now, rule q applies to state s iff $v(s)+v(q)\in {\mathbb{\mathbb{N}}}^n$ (all components of the vector are ≥0) and if $s\to t$ then $v(t)=v(s)+v(q)$. So the fractran multiplication model is completely equivalent to the vector adding model. For presentation, we will represent a fractran program with a matrix where each row is the vector representation for a rule.

For example, the BBf(15) champion ([1/45, 4/5, 3/2, 25/3]) in vector representation would be:

$$\left[\begin{array}{ccc}0& -2& -1\\ 2& 0& -1\\ -1& 1& 0\\ 0& -1& 2\end{array}\right]$$

In this representation, it becomes much easier to reason about fractran programs and describe general rules. It is also very easy to calculate the size of a rule or program in vector representation. It is the sum of absolute values of all elements in the matrix + number of rules (number of rows).

Relationship to VAS / Petri Nets

Using vector representation, fractran programs are a deterministic version of Vector Addition Systems (VAS) (and, equivalently, Petri Nets). VAS are identical to fractran programs in vector representation except that the rules are unordered and non-deterministic, they are used to model distributed systems where precise order of rule execution cannot be predicted. Interestingly, many problems about VAS are actually decidable, but their runtimes are extremely slow. Notably, the reachability problem (given states A and B are there a sequence of rules so that $A{\to }^{*}B$) is "Ackermann-complete" meaning that the optimal algorithm has worst-case runtime akin to the famously fast-growing Ackermann function.

Deciders

All Fractran deciders summarized and their relations, shared by Daniel Yuan on 14 Nov 2025

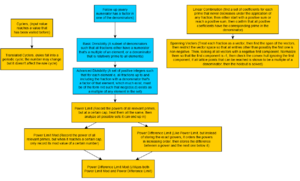
Many specialized deciders have been invented to prove fractran programs non-halting. See image at right.

Champions

The table of champions is split into two pieces: the first for small champions (up to BBf(14)) which all share the same relatively simple behavior (sequential programs) is collapsed by default; the second for champions BBf(15) and beyond which have more complex and varied behavior.

All small champions as well as the first few larger ones were discovered and proven maximal by Jason Yuen (@-d) in their initial enumeration on 1 Nov 2025.

Small Champions

n	BBf(n)	Example Champion	Vector Representation
2	1	[1/2]	$\left[\begin{array}{c}-1\end{array}\right]$
3	1	[3/2]	$\left[\begin{array}{cc}-1& 1\end{array}\right]$
4	1	[9/2]	$\left[\begin{array}{cc}-1& 2\end{array}\right]$
5	2	[3/2, 1/3]	$\left[\begin{array}{cc}-1& 1\\ 0& -1\end{array}\right]$
6	3	[9/2, 1/3]	$\left[\begin{array}{cc}-1& 2\\ 0& -1\end{array}\right]$
7	4	[27/2, 1/3]	$\left[\begin{array}{cc}-1& 3\\ 0& -1\end{array}\right]$
8	5	[81/2, 1/3]	$\left[\begin{array}{cc}-1& 4\\ 0& -1\end{array}\right]$
9	6	[243/2, 1/3]	$\left[\begin{array}{cc}-1& 5\\ 0& -1\end{array}\right]$
10	7	[729/2, 1/3]	$\left[\begin{array}{cc}-1& 6\\ 0& -1\end{array}\right]$
11	10	[27/2, 25/3, 1/5]	$\left[\begin{array}{ccc}-1& 3& 0\\ 0& -1& 2\\ 0& 0& -1\end{array}\right]$
12	13	[81/2, 25/3, 1/5]	$\left[\begin{array}{ccc}-1& 4& 0\\ 0& -1& 2\\ 0& 0& -1\end{array}\right]$
13	17	[81/2, 125/3, 1/5]	$\left[\begin{array}{ccc}-1& 4& 0\\ 0& -1& 3\\ 0& 0& -1\end{array}\right]$
14	21	[243/2, 125/3, 1/5]	$\left[\begin{array}{ccc}-1& 5& 0\\ 0& -1& 3\\ 0& 0& -1\end{array}\right]$

n	BBf(n)	Example Champion	Vector Representation	Champion Found	Holdouts Proven
15	28	[1/45, 4/5, 3/2, 25/3]	$\left[\begin{array}{ccc}0& -2& -1\\ 2& 0& -1\\ -1& 1& 0\\ 0& -1& 2\end{array}\right]$	Jason Yuen (@-d) 1 Nov 2025	Jason Yuen (@-d) 1 Nov 2025
16	53	[1/45, 4/5, 3/2, 125/3]	$\left[\begin{array}{ccc}0& -2& -1\\ 2& 0& -1\\ -1& 1& 0\\ 0& -1& 3\end{array}\right]$	Jason Yuen (@-d) 1 Nov 2025	Jason Yuen (@-d) 1 Nov 2025
17	107	[5/6, 49/2, 3/5, 40/7]	$\left[\begin{array}{cccc}-1& -1& 1& 0\\ -1& 0& 0& 2\\ 0& 1& -1& 0\\ 3& 0& 1& -1\end{array}\right]$	Jason Yuen (@-d) 1 Nov 2025	Daniel Yuan (@dyuan01) 3 Nov 2025
18	211	[5/6, 49/2, 3/5, 80/7]	$\left[\begin{array}{cccc}-1& -1& 1& 0\\ -1& 0& 0& 2\\ 0& 1& -1& 0\\ 4& 0& 1& -1\end{array}\right]$	Jason Yuen (@-d) 4 Nov 2025	Jason Yuen (@-d) 8 Nov 2025
19	370	[5/6, 49/2, 3/5, 160/7]	$\left[\begin{array}{cccc}-1& -1& 1& 0\\ -1& 0& 0& 2\\ 0& 1& -1& 0\\ 5& 0& 1& -1\end{array}\right]$	@creeperman7002 5 Nov 2025	Decider: Daniel Yuan (@dyuan01) 13 Nov 2025 3 Holdouts: Racheline & Shawn Ligocki
20	≥ 746	[7/15, 22/3, 6/77, 5/2, 9/5]	$\left[\begin{array}{ccccc}0& -1& -1& 1& 0\\ 1& -1& 0& 0& 1\\ 1& 1& 0& -1& -1\\ -1& 0& 1& 0& 0\\ 0& 2& -1& 0& 0\end{array}\right]$	Jason Yuen (@-d) 13 Nov 2025	29 holdouts[1] remain. 7 Dec 2025
21	≥ 31,957,632	[7/15, 4/3, 27/14, 5/2, 9/5]	$\left[\begin{array}{cccc}0& -1& -1& 1\\ 2& -1& 0& 0\\ -1& 3& 0& -1\\ -1& 0& 1& 0\\ 0& 2& -1& 0\end{array}\right]$	Jason Yuen (@-d) 16 Nov 2025	602 holdouts[2] remain. 25 Nov 2025
22	$>1.146\times 10^{62}$	[1/12, 9/10, 14/3, 11/2, 5/7, 3/11]	$\left[\begin{array}{ccccc}-2& -1& 0& 0& 0\\ -1& 2& -1& 0& 0\\ 1& -1& 0& 1& 0\\ -1& 0& 0& 0& 1\\ 0& 0& 1& -1& 0\\ 0& 1& 0& 0& -1\end{array}\right]$	Shawn Ligocki (@sligocki) 11 Dec 2025 and Jason Yuen (@-d) [3]	10458 holdouts[4] remain. 11 Dec 2025
23					Known Cryptids: Frankenstein's Monster Antihydra-like Cryptid

Behavior of Champions

Sequential programs

All champions up to BBf(14) have very simple behavior. They are all of the form: $[\frac{3^{a_1}}{2},\frac{5^{a_2}}{3},...\frac{p_n^{a_k}}{p_{k-1}},\frac{1}{p_k}]$ or in vector representation (limited to k=4):

$$\left[\begin{array}{ccccc}-1& a_1& 0& 0& 0\\ 0& -1& a_2& 0& 0\\ 0& 0& -1& a_3& 0\\ 0& 0& 0& -1& a_4\\ 0& 0& 0& 0& -1\end{array}\right]$$

These champions repeatedly apply the rules in sequence, never going back to a previous rule. They apply the first rule until they've exhausted all 2s, then the second rule until they've exhausted all 3s, etc. They have a runtime of $1+a_1+a_1{a}_2+a_1{a}_2{a}_3+\cdots =\sum _{i=0}^k\prod _{j=1}^i{a}_j$ and size $2k+2+\sum _{i=1}^k{a}_i$. This grows linearly for k=1 (BBf(5) to BBf(10)) and quadratically for k=2 (BBf(11) to BBf(14)). Letting k grow with the size, the maximum runtime grows exponentially in the program size.

BBf(15) Family

The BBf(15) and BBf(16) champions are members of a family of programs (parameterized by $n\ge 1$):

$$\left[\begin{array}{ccc}0& -2& -1\\ 2& 0& -1\\ -1& 1& 0\\ 0& -1& n\end{array}\right]$$

Let a = 2, b = 3, and c = 5.

The BBf(15) champion (n = 2) implements this iteration:

$$\begin{array}{lcl}{b}^0& \stackrel{0}{\to }& \text{halt}\\ b^1& \stackrel{7}{\to }& b^4\\ b^2& \stackrel{7}{\to }& b^5\\ b^3& \stackrel{5}{\to }& b^2\\ b^4& \stackrel{5}{\to }& b^3\\ b^{n+5}& \stackrel{3}{\to }& b^n\\ \end{array}$$

which follows a permutation-like trajectory: $a\stackrel{1}{\to }{b}^1\to b^4\to b^3\to b^2\to b^5\to b^0\to \text{halt}$

The BBf(16) champion (n = 3) implements this iteration:

$$\begin{array}{lcl}{b}^0& \stackrel{0}{\to }& \text{halt}\\ b^1& \stackrel{10}{\to }& b^6\\ b^2& \stackrel{10}{\to }& b^7\\ b^3& \stackrel{8}{\to }& b^4\\ b^4& \stackrel{8}{\to }& b^5\\ b^5& \stackrel{6}{\to }& b^2\\ b^6& \stackrel{6}{\to }& b^3\\ b^{n+7}& \stackrel{4}{\to }& b^n\\ \end{array}$$

which follows a permutation-like trajectory: $a\stackrel{1}{\to }{b}^1\to b^6\to b^3\to b^4\to b^5\to b^2\to b^7\to b^0\to \text{halt}$

BBf(17) Family

The BBf(17) to BBf(19) champions are members of a family of programs (parameterized by $m,n\ge 0$)

$$\left[\begin{array}{cccc}-1& -1& 1& 0\\ -1& 0& 0& n\\ 0& 1& -1& 0\\ m& 0& 1& -1\end{array}\right]$$

which have size $m+n+12$

This family obeys the following rules:

1. $[1,0,0,0]\stackrel{1}{\to }[0,0,0,n]$
2. if d≥1 and b≤m:$$[0,b,0,d]\stackrel{m+b+2}{\to }[0,b+1,0,d-1+n(m-b)]$$
3. if d≥1 and b≥m:$$[0,b,0,d]\stackrel{2m+2}{\to }[0,b+1,0,d-1]$$
4. if d=0: [0,b,0,d] has halted

and furthermore these rules are applied in order since b is always increasing (and d is eventually decreasing). Combining these together we get runtime:$$1+n(m+1)(m(m+1)+2)-\frac{m(m+1)}{2}$$

The optimal choices for n,m for various program sizes are:

Size	n	m	Runtime
16	1	3	51
17	2	3	107
18	2	4	211
19	2	5	370
20	2	6	596
21	3	6	904

BBf(20)

The BBf(20) champion (running 746 steps):

$$\left[\begin{array}{ccccc}0& -1& -1& 1& 0\\ 1& -1& 0& 0& 1\\ 1& 1& 0& -1& -1\\ -1& 0& 1& 0& 0\\ 0& 2& -1& 0& 0\end{array}\right]$$

This program implements a Collatz-like iteration. Let $C(n)=[0,0,n,2,0]$, then:

$$\begin{array}{lcl}[1,0,0,0,0]& \stackrel{49}{\to }& C(2)\\ C(3k)& \stackrel{3k}{\to }& \text{halt}\\ C(3k+1)& \stackrel{11k+22}{\to }& C(4k+3)\\ C(3k+2)& \stackrel{11k+22}{\to }& C(4k+4)\\ \end{array}$$

which follows the reasonably "lucky" trajectory:

$$C(2)\to C(4)\to C(7)\to C(11)\to C(16)\to C(23)\to C(32)\to C(44)\to C(60)\to \text{halt}$$

BBf(21)

The BBf(21) champion (running >31M steps): $$\left[\begin{array}{cccc}0& -1& -1& 1\\ 2& -1& 0& 0\\ -1& 3& 0& -1\\ -1& 0& 1& 0\\ 0& 2& -1& 0\end{array}\right]$$

This program implements a Collatz-like iteration. Let $D(n)=[0,0,n,0]$, then:^[5] $$\begin{array}{lcl}[1,0,0,0,0]& \stackrel{1}{\to }& D(1)\\ D(3k)& \stackrel{k}{\to }& \text{halt}\\ D(3k+1)& \stackrel{21k+7}{\to }& C(10k+4)\\ D(3k+2)& \stackrel{21k+14}{\to }& C(10k+7)\\ \end{array}$$

which follows the reasonably "lucky" trajectory: $$\begin{array}{ll}D(1)& \to D(4)\to D(14)\to D(47)\to D(157)\to D(524)\to D(1747)\to D(5824)\to D(19414)\\ & \to D(64714)\to D(215714)\to D(719047)\to D(2396824)\to D(7989414)\to \text{halt}\\ \end{array}$$

BBf(22)

The BBf(22) champion (running $>10^{62}$ steps): $$\left[\begin{array}{ccccc}-2& -1& 0& 0& 0\\ -1& 2& -1& 0& 0\\ 1& -1& 0& 1& 0\\ -1& 0& 0& 0& 1\\ 0& 0& 1& -1& 0\\ 0& 1& 0& 0& -1\end{array}\right]$$

This program implements a Collatz-like unbiased psuedo-random walk. Let $S(x,y)=[0,0,x,0,y]$, then:^[6] $$\begin{array}{lcl}[1,0,0,0,0]& \stackrel{1}{\to }& S(0,1)\\ S(x,0)& =& \text{halt}\\ S(3k,y+1)& \stackrel{14k+4}{\to }& S(5k+1,y+1)\\ S(3k+1,y+1)& \stackrel{14k+10}{\to }& S(5k+3,y+2)\\ S(3k+2,y+1)& \stackrel{14k+12}{\to }& S(5k+4,y)\\ \end{array}$$

This random walk iterates 275 times until it halts reaching a maximum y value of 14 at iteration 111: $$\begin{array}{ll}S(0,1)& \to S(1,1)\to S(3,2)\to S(6,2)\to S(11,2)\to S(19,1)\to S(33,2)\to S(56,2)\to S(94,1)\\ & \to S(158,2)\to S(264,1)\to S(441,1)\to S(736,1)\to S(1228,2)\to S(2048,3)\\ & ⋮\\ & \to S(4065328691604230522442358,13)\\ & \to S(6775547819340384204070598,14)\\ & \to S(11292579698900640340117664,13)\\ & ⋮\\ & \to S(27930059557111373800280446055462487109112535227834136644,2)\\ & \to S(46550099261852289667134076759104145181854225379723561074,1)\\ & \to S(77583498769753816111890127931840241969757042299539268458,2)\\ & \to S(129305831282923026853150213219733736616261737165898780764,1)\\ & \to S(215509718804871711421917022032889561027102895276497967941,1)\\ & \to S(359182864674786185703195036721482601711838158794163279903,2)\\ & ⋮\\ & \to S(5894430516013404355095519889620117404469367857588232386361874,2)\\ & \to S(9824050860022340591825866482700195674115613095980387310603124,1)\\ & \to S(16373418100037234319709777471166992790192688493300645517671874,0)\end{array}$$

Cryptids

Frankenstein's Monster

"Frankenstein's Monster" is a size 23 Cryptid. It was created by tweaking a single instruction in the size 22 champion. This tweak switches it from a unbiased random walk to a biased one and thus makes halting probviously impossible. It is called Frankenstein's Monster since it was found by a combination of exhaustive search and hand design.^[7]

[1/12, 9/10, 14/3, 121/2, 5/7, 3/11] $$\left[\begin{array}{ccccc}-2& -1& 0& 0& 0\\ -1& 2& -1& 0& 0\\ 1& -1& 0& 1& 0\\ -1& 0& 0& 0& 2\\ 0& 0& 1& -1& 0\\ 0& 1& 0& 0& -1\end{array}\right]$$

It's behavior is extremely similar to the size 22 champion:

$$\begin{array}{lcl}[1,0,0,0,0]& \stackrel{1}{\to }& S(0,2)\\ S(x,0)& =& \text{halt}\\ S(3k,y+1)& \stackrel{14k+4}{\to }& S(5k+1,y+2)\\ S(3k+1,y+1)& \stackrel{14k+10}{\to }& S(5k+3,y+4)\\ S(3k+2,y+1)& \stackrel{14k+12}{\to }& S(5k+4,y)\\ \end{array}$$

with the only difference that the y values now change by {+1,+3,-1} depending on the value of x mod 3 (instead of {0,+1,-1} in the original size 22 program). The x values follow the exact same path as in the original size 22 champion, but the y values quickly grow linearly with the number of iterations (as expected by the random model):

         0: S(0, 1)  @ 1  (0.00s)
   100_000: S(10^22_185, 100171)  @ 10^22_186  (0.87s)
   200_000: S(10^44_370, 200187)  @ 10^44_371  (3.42s)
   300_000: S(10^66_555, 300759)  @ 10^66_556  (7.68s)
   400_000: S(10^88_740, 400451)  @ 10^88_741  (13.64s)
   500_000: S(10^110_925, 500421)  @ 10^110_925  (21.28s)
   600_000: S(10^133_109, 600351)  @ 10^133_110  (30.62s)
   700_000: S(10^155_294, 700319)  @ 10^155_295  (41.64s)
   800_000: S(10^177_479, 799911)  @ 10^177_480  (54.30s)
   900_000: S(10^199_664, 900259)  @ 10^199_665  (68.59s)
 1_000_000: S(10^221_849, 1000853)  @ 10^221_850  (84.51s)
...

 4_000_000: S(10^887_395, 4000201)  @ 10^887_396  (1474.02s)
...

Antihydra-like Cryptid

This Cryptid is a size 23 Cryptid. This Cryptid was constructed by Maksandchael by tweaking Frankenstein's Monster to make it as similar to Antihydra as possible. [9/10, 1/6, 1331/2, 14/3, 5/7, 3/11].

H(a, b) = [0, 0, a-2, 0, b]
Start -> H(2, 3)
H(2a, b) -> H(3a, b+2)
H(2a+1, b+1) -> H(3a+1, b)
H(a,0) -> halt

Hydra

A size 29 program was produced by hand to simulates Hydra rules (Discord):

[507/22, 26/33, 245/2, 5/21, 1/3, 11/13, 22/5] $$\left[\begin{array}{cccccc}-1& 1& 0& 0& -1& 2\\ 1& -1& 0& 0& -1& 1\\ -1& 0& 1& 2& 0& 0\\ 0& -1& 1& -1& 0& 0\\ 0& -1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& -1\\ 1& 0& -1& 0& 1& 0\end{array}\right]$$

The intended interpretation is that if we let $S(h,w)=[1,0,0,w,h-3,0]$ then it follows the following rules:

$$\begin{array}{lcl}[1,0,\dots ]& =& S(3,0)\\ S(2k,0)& {\to }^{*}& \text{halt}\\ S(2k,w+1)& {\to }^{*}& S(3k,w)\\ S(2k+1,w)& {\to }^{*}& S(3k+1,w+2)\\ \end{array}$$

BMO1

A size 36 program was produced by hand to simulate BMO1 rules (Discord):

[153/55, 2/11, 26/35, 3/7, 11/17, 7/13, 25/6, 55/2, 14/3] $$\left[\begin{array}{ccccccc}0& 2& -1& 0& -1& 0& 1\\ 1& 0& 0& 0& -1& 0& 0\\ 1& 0& -1& -1& 0& 1& 0\\ 0& 1& 0& -1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& -1\\ 0& 0& 0& 1& 0& -1& 0\\ -1& -1& 2& 0& 0& 0& 0\\ -1& 0& 1& 0& 1& 0& 0\\ 1& -1& 0& 1& 0& 0& 0\end{array}\right]$$

Let $A(a,b)=[a,b,0,0,0,0,0]$, then it follows the rules:

$$\begin{array}{lcl}[1,0,\dots ]& {\to }^{*}& A(1,2)\\ A(a,b)& {\to }^{*}& A(a-b,4b+2)& \text{if }a>b\\ A(a,b)& {\to }^{*}& A(2a+1,b-a)& \text{if }a<b\\ A(a,b)& {\to }^{*}& \text{Halt}& \text{if }a=b\\ \end{array}$$

BMO 6 (“Space Needle”)

A size 48 program was produced by hand to simulate BMO 6 rules (Discord)

[77/2, 2/99, 17/33, 13/11, 285/119, 17/19, 1375/51, 1/17, 3/5, 243/7, 10/13]

$\left[\begin{array}{cccccccc}-1& 0& 0& 1& 1& 0& 0& 0\\ 1& -2& 0& 0& -1& 0& 0& 0\\ 0& -1& 0& 0& -1& 0& 1& 0\\ 0& 0& 0& 0& -1& 1& 0& 0\\ 0& 1& 1& -1& 0& 0& -1& 1\\ 0& 0& 0& 0& 0& 0& 1& -1\\ 0& -1& 3& 0& 1& 0& -1& 0\\ 0& 0& 0& 0& 0& 0& -1& 0\\ 0& 1& -1& 0& 0& 0& 0& 0\\ 0& 5& 0& -1& 0& 0& 0& 0\\ 1& 0& 1& 0& 0& -1& 0& 0\end{array}\right]$

A(a, b) = B^a C^b E or B^(a-2) C^b D E

Start: A(7, 1)

A(1, b) --> halt

A(2a, b) --> A(5a+b+2, 1)

A(2a+1, b) --> A(b-1, b+c+3)