BB(6): Difference between revisions
m add classic cryptid #5 |
RobinCodes (talk | contribs) →Holdouts: Updated simulation progress |
||
| (75 intermediate revisions by 15 users not shown) | |||
| Line 1: | Line 1: | ||
The 6-state, 2-symbol Busy Beaver problem '''BB(6)''' | The 6-state, 2-symbol Busy Beaver problem, '''BB(6)''', refers to the unsolved 6<sup>th</sup> value of the [[Busy Beaver function]]. With the discovery of the [[Cryptid]] machine [[Antihydra]] in June 2024, we now know that we must solve a [[Collatz-like]] problem in order to solve BB(6) and thus [https://www.sligocki.com/2024/07/06/bb-6-2-is-hard.html BB(6) is Hard]. | ||
The current BB(6) champion {{TM| | The current BB(6) [[champion]] {{TM|1RB1RA_1RC1RZ_1LD0RF_1RA0LE_0LD1RC_1RA0RE|halt}} was discovered by mxdys in June 2025, proving the lower bound: | ||
<math display="block">S(6) > \Sigma(6) > | <math display="block">S(6) > \Sigma(6) > 2 \uparrow\uparrow\uparrow 5</math> | ||
== Techniques == | == Techniques == | ||
Simulating tetrational machines, such as the former champion {{TM|1RB0LD_1RC0RF_1LC1LA_0LE1RZ_1LF0RB_0RC0RE|halt}}, requires [[Accelerated simulator|accelerated simulation]] that can handle Collatz Level 2 [[Inductive rule|inductive rules]]. In other words, it requires a simulator that can prove the rules: | |||
<math display="block">\begin{array}{ | <math display="block">\begin{array}{lcl} | ||
C(4k) & \to & Halt(\frac{3^{k+3} - 11}{2}) \\ | C(4k) & \to & {\operatorname{Halt}}\Big(\frac{3^{k+3} - 11}{2}\Big) \\ | ||
C(4k+1) & \to & C(\frac{3^{k+3} - 11}{2}) \\ | C(4k+1) & \to & C\Big(\frac{3^{k+3} - 11}{2}\Big) \\ | ||
C(4k+2) & \to & C(\frac{3^{k+3} - 11}{2}) \\ | C(4k+2) & \to & C\Big(\frac{3^{k+3} - 11}{2}\Big) \\ | ||
C(4k+3) & \to & C(\frac{3^{k+3} + 1}{2}) \\ | C(4k+3) & \to & C\Big(\frac{3^{k+3} + 1}{2}\Big) \\ | ||
\end{array}</math> | \end{array}</math> | ||
and also compute the remainder mod 3 of numbers produced by applying these rules 15 times (which requires some fancy math related to [[wikipedia:Euler's_totient_function|Euler' | and also compute the remainder mod 3 of numbers produced by applying these rules 15 times (which requires some fancy math related to [[wikipedia:Euler's_totient_function|Euler's totient function]]). | ||
We are also applying existing automatic deciders on current holdout lists with more extreme choices of parameters (more computational resources). [[User:XnoobSpeakable|XnoobSpeakable]] was able to solve 11 of the final 2728 holdouts using higher order parameters with the Ligockis' Enumerate.py. An example command line entry is: | |||
<syntaxhighlight lang="bash"> | |||
python3 Code/Enumerate.py --infile "bb6in/bb6tm{i}.txt" --outfile "bb6out/t{i}.pb" -r --no-steps --exp-linear-rules --max-loops=50_000_000 --block-mult=3 --max-block-size=100 --time=500 --force --save-freq=1 | |||
</syntaxhighlight> | |||
XnoobSpeakable ran Enumerate.py on all TMs in the 2728 holdout list with the above max-loops and max-block-size parameters using <code>--block-mult=1</code> ,<code>--block-mult=2</code> , and <code>--block-mult=3</code>. For context, during the Stage 2 BB(7) enumeration, where speed was more important due to the tens of millions of known holdouts, parameters of <code>--max-loops=100_000 --block-mult=2 --time=30 --save-freq=100</code> were used. | |||
@Iijil's [[MITMWFAR|MITMWFAR decider]] is likely too weak to be of any assistance: running the decider on 2650 BB(6) holdouts, using parameters not strong enough to solve BB(5) TMs, took prohibitively long to compute. Instead, [https://discord.com/channels/960643023006490684/1028746861395316776/1442964185599447152 a new FAR method] by mxdys was able to decide 113 of the 1534 holdouts. | |||
== Cryptids == | == Cryptids == | ||
Several [[Turing machines]] have been found that are [[Cryptids]], considered so because each of them have a [[Collatz-like]] halting problem, a type of problem that is generally difficult to solve. However, probabilistic arguments have allowed all but one of them to be categorized as [[probviously]] halting or probviously non-halting. | |||
Probviously non-halting Cryptids: | |||
* {{TM|1RB1RA_0LC1LE_1LD1LC_1LA0LB_1LF1RE_---0RA}}, [[Antihydra]] | |||
* {{TM|1RB1RC_1LC1LE_1RA1RD_0RF0RE_1LA0LB_---1RA|undecided}}, a variant of [[Hydra]] and Antihydra | |||
* {{TM|1RB1LD_1RC1RE_0LA1LB_0LD1LC_1RF0RA_---0RC|undecided}}, similar to Antihydra | |||
* {{TM|1RB0LD_1RC1RF_1LA0RA_0LA0LE_1LD1LA_0RB---|undecided}}, similar to Antihydra | |||
* {{TM|1RB0LB_1LC0RE_1LA1LD_0LC---_0RB0RF_1RE1RB|undecided}}, similar to Antihydra | |||
* {{TM|1RB1LA_1LC0RE_1LF1LD_0RB0LA_1RC1RE_---0LD|undecided}} | |||
Probviously halting Cryptids: | |||
* {{TM|1RB0RD_0RC1RE_1RD0LA_1LE1LC_1RF0LD_---0RA}}, [[Lucy's Moonlight]] | |||
* {{TM|1RB1RA_0RC1RC_1LD0LF_0LE1LE_1RA0LB_---0LC|undecided}}, a family of 16 related TMs | |||
* {{TM|1RB1RE_1LC1LD_---1LA_1LB1LE_0RF0RA_1LD1RF}} | |||
* {{TM|1RB0RE_1LC1LD_0RA0LD_1LB0LA_1RF1RA_---1LB}} | |||
* {{TM|1RB0LC_0LC0RF_1RD1LC_0RA1LE_---0LD_1LF1LA}} | |||
* {{TM|1RB0LC_1LC0RD_1LF1LA_1LB1RE_1RB1LE_---0LE}} | |||
* {{TM|1RB---_0RC0RE_1RD1RF_1LE0LB_1RC0LD_1RC1RA}} | |||
* {{TM|1RB0LD_1RC1RA_1LD0RB_1LE1LA_1RF0RC_---1RE}} | |||
* {{TM|1RB1LD_1RC0LE_1LA1RE_0LF1LA_1RB0RB_---0LB}} | |||
* {{TM|1RB0RE_1LC0RA_1LA1LD_1LC1LF_0LC0LB_1LE---}} | |||
Although {{TM|1RB1LE_0LC0LB_1RD1LC_1RD1RA_1RF0LA_---1RE}} behaves similarly to the probviously halting Cryptids, it is estimated to have a 3/5 chance of becoming a [[translated cycler]] and a 2/5 chance of halting. | |||
There are a few machines considered notable for their chaotic behaviour, but which have not been classified as Cryptids due to seemingly lacking a connection to any known open mathematical problems, such as Collatz-like problems. | |||
Potential Cryptids: | Potential Cryptids: | ||
| Line 32: | Line 59: | ||
* {{TM|1RB0LD_1LC0RA_1RA1LB_1LA1LE_1RF0LC_---0RE|undecided}} | * {{TM|1RB0LD_1LC0RA_1RA1LB_1LA1LE_1RF0LC_---0RE|undecided}} | ||
* {{TM|1RB0RB_1LC1RE_1LF0LD_1RA1LD_1RC1RB_---1LC|undecided}} | * {{TM|1RB0RB_1LC1RE_1LF0LD_1RA1LD_1RC1RB_---1LC|undecided}} | ||
* {{TM|1RB0LD_0RC0RE_1LC0LA_---1LE_0LF0RE_0RA0LE|undecided}} | |||
* {{TM|1RB1RF_1LC1LF_0RE1LD_0LB1LD_---1RC_1RA0RD|undecided}} | |||
== Top Halters == | == Top Halters == | ||
Below is a table of the machines with the 20 highest known runtimes.<ref>Shawn Ligocki's list of 6-state, 2-symbol machines with large runtimes ([https://github.com/sligocki/busy-beaver/blob/main/Machines/bb/6x2.txt Link])</ref> Their sigma scores are expressed using an extension of [[wikipedia:Knuth's_up-arrow_notation|Knuth's up-arrow notation]].<ref>Shawn Ligocki. 2022. [https://www.sligocki.com/2022/06/25/ext-up-notation.html "Extending Up-arrow Notation"]</ref> | |||
1RB0LD_1RC0RF_1LC1LA_0LE1RZ_1LF0RB_0RC0RE | {| class="wikitable" | ||
1RB0LA_1LC1LF_0LD0LC_0LE0LB_1RE0RA_1RZ1LD | |+Top Known BB(6) Halters | ||
1RB1RE_1LC1LF_1RD0LB_1LE0RC_1RA0LD_1RZ1LC | !Standard format | ||
1RB0LE_0RC1RA_0LD1RF_1RE0RB_1LA0LC_0RD1RZ | !(approximate) Σ | ||
1RB0RF_1LC1LB_0RE0LD_0LC0LB_0RA1RE_0RD1RZ | !Discoverer | ||
1RB1LA_1LC0RF_1LD1LC_1LE0RE_0RB0LC_1RZ1RA | |- | ||
1RB0LE_1LC1RA_1RE0LD_1LC1LF_1LA0RC_1RZ1LC | |{{TM|1RB1RA_1RC1RZ_1LD0RF_1RA0LE_0LD1RC_1RA0RE|halt}} | ||
1RB1RF_1LC1RE_0LD1LB_1LA0RA_0RA0RB_1RZ0RD | |2 ↑↑↑ 5 | ||
1RB0LF_1LC0RA_1RD0LB_1LE1RC_1RZ1LA_1LA1LE | |mxdys | ||
1RB1RZ_0LC0LD_1LD1LC_1RE1LB_1RF1RD_0LD0RA | |- | ||
</ | |{{TM|1RB1LC_1LA1RE_0RD0LA_1RZ1LB_1LD0RF_0RD1RB|halt}} | ||
|10 ↑↑ 11010000 | |||
|mxdys | |||
|- | |||
|{{TM|1RB0LD_1RC0RF_1LC1LA_0LE1RZ_1LF0RB_0RC0RE|halt}} | |||
|10 ↑↑ 15.60465 | |||
|Pavel Kropitz | |||
|- | |||
|{{TM|1RB0LF_1RC1RB_1LD0RA_1LB0LE_1RZ0LC_1LA1LF|halt}} | |||
|10 ↑↑ 7.52390 | |||
| | |||
|- | |||
|{{TM|1RB0LF_1RC1RB_1LD0RA_1RF0LE_1RZ0LC_1LA1LF|halt}} | |||
|10 ↑↑ 7.52390 | |||
| | |||
|- | |||
|{{TM|1RB0LF_1RC1RB_1LD0RA_1LF0LE_1RZ0LC_1LA1LF|halt}} | |||
|10 ↑↑ 7.52390 | |||
| | |||
|- | |||
|{{TM|1RB1RC_1LC1RE_1LD0LB_1RE1LC_1LE0RF_1RZ1RA|halt}} | |||
|10 ↑↑ 7.23619 | |||
| | |||
|- | |||
|{{TM|1RB1RA_1LC1LE_1RE0LD_1LC0LF_1RZ0RA_0RA0LB|halt}} | |||
|10 ↑↑ 6.96745 | |||
|poppuncher | |||
|- | |||
|{{TM|1RB0RF_1LC0RA_1RZ0LD_1LE1LD_1RB1RC_0LD0RE|halt}} | |||
|10 ↑↑ 5.77573 | |||
|poppuncher | |||
|- | |||
|{{TM|1RB0LA_1LC1LF_0LD0LC_0LE0LB_1RE0RA_1RZ1LD|halt}} | |||
|10 ↑↑ 5.63534 | |||
|Shawn Ligocki | |||
|- | |||
|{{TM|1RB1RE_1LC1LF_1RD0LB_1LE0RC_1RA0LD_1RZ1LC|halt}} | |||
|10 ↑↑ 5.56344 | |||
| | |||
|- | |||
|{{TM|1RB0LE_0RC1RA_0LD1RF_1RE0RB_1LA0LC_0RD1RZ|halt}} | |||
|10 ↑↑ 5.12468 | |||
| | |||
|- | |||
|{{TM|1RB0RF_1LC1LB_0RE0LD_0LC0LB_0RA1RE_0RD1RZ|halt}} | |||
|10 ↑↑ 5.03230 | |||
| | |||
|- | |||
|{{TM|1RB1LA_1LC0RF_1LD1LC_1LE0RE_0RB0LC_1RZ1RA|halt}} | |||
|10 ↑↑ 4.91072 | |||
| | |||
|- | |||
|{{TM|1RB0LE_1LC1RA_1RE0LD_1LC1LF_1LA0RC_1RZ1LC|halt}} | |||
|10 ↑↑ 3.33186 | |||
| | |||
|- | |||
|{{TM|1RB1RF_1LC1RE_0LD1LB_1LA0RA_0RA0RB_1RZ0RD|halt}} | |||
|10 ↑↑ 3.31128 | |||
| | |||
|- | |||
|{{TM|1RB0LF_1LC0RA_1RD0LB_1LE1RC_1RZ1LA_1LA1LE|halt}} | |||
|10 ↑↑ 3.18855 | |||
| | |||
|- | |||
|{{TM|1RB0RF_1LC1RB_0RD0LB_1RZ0LE_1RE0RA_1RD1RE|halt}} | |||
|10 ↑↑ 3.16005 | |||
| | |||
|- | |||
|{{TM|1RB1RZ_0LC0LD_1LD1LC_1RE1LB_1RF1RD_0LD0RA|halt}} | |||
|<math>10^{646\,456\,993}</math> | |||
|Pavel Kropitz | |||
|- | |||
|{{TM|1RB0RC_0LC0LB_0LD1LC_0LE1LA_0LF---_1RF1RA|halt}} | |||
|<math>> 10^{11\,952\,340}</math> (lower bound) | |||
|Racheline | |||
|} | |||
The runtimes are presumed to be about <math>\text{score}^2</math> which is roughly indistinguishable in tetration notation. | |||
== Holdouts == | == Holdouts == | ||
@mxdys's informal [[Holdouts lists|holdouts list]] | [[File:BB(6) holdouts decrease over time.png|alt=BB(6) Holdouts count decrease overtime.|thumb|Number of BB(6) holdouts over time.]] | ||
@mxdys's informal [[Holdouts lists|holdouts list]] has 1326 machines up to equivalence as of December 2025. Partial Rocq proof is [https://github.com/ccz181078/busycoq/tree/BB6 available on Github]. | |||
Always up-to-date annotated spreadsheet, with links to Discord discussions: [https://docs.google.com/spreadsheets/d/1mMp8bAcTFT91j7azn72liX8NSTwc2E_ozKnOGTfRCfw/edit?gid=1330361301#gid=1330361301 Spreadsheet]. | |||
All holdouts have been simulated up to at least 1e12 steps. 210 holdouts have not been simulated out to 1e13 steps. (The list can be found in the spreadsheet) | |||
== References == | == References == | ||
<references /> | <references /> | ||
[[Category:BB Domains]][[Category:BB(6)]] | |||
Latest revision as of 17:37, 7 January 2026
The 6-state, 2-symbol Busy Beaver problem, BB(6), refers to the unsolved 6th value of the Busy Beaver function. With the discovery of the Cryptid machine Antihydra in June 2024, we now know that we must solve a Collatz-like problem in order to solve BB(6) and thus BB(6) is Hard.
The current BB(6) champion 1RB1RA_1RC1RZ_1LD0RF_1RA0LE_0LD1RC_1RA0RE (bbch) was discovered by mxdys in June 2025, proving the lower bound:
Techniques
Simulating tetrational machines, such as the former champion 1RB0LD_1RC0RF_1LC1LA_0LE1RZ_1LF0RB_0RC0RE (bbch), requires accelerated simulation that can handle Collatz Level 2 inductive rules. In other words, it requires a simulator that can prove the rules:
and also compute the remainder mod 3 of numbers produced by applying these rules 15 times (which requires some fancy math related to Euler's totient function).
We are also applying existing automatic deciders on current holdout lists with more extreme choices of parameters (more computational resources). XnoobSpeakable was able to solve 11 of the final 2728 holdouts using higher order parameters with the Ligockis' Enumerate.py. An example command line entry is:
python3 Code/Enumerate.py --infile "bb6in/bb6tm{i}.txt" --outfile "bb6out/t{i}.pb" -r --no-steps --exp-linear-rules --max-loops=50_000_000 --block-mult=3 --max-block-size=100 --time=500 --force --save-freq=1
XnoobSpeakable ran Enumerate.py on all TMs in the 2728 holdout list with the above max-loops and max-block-size parameters using --block-mult=1 ,--block-mult=2 , and --block-mult=3. For context, during the Stage 2 BB(7) enumeration, where speed was more important due to the tens of millions of known holdouts, parameters of --max-loops=100_000 --block-mult=2 --time=30 --save-freq=100 were used.
@Iijil's MITMWFAR decider is likely too weak to be of any assistance: running the decider on 2650 BB(6) holdouts, using parameters not strong enough to solve BB(5) TMs, took prohibitively long to compute. Instead, a new FAR method by mxdys was able to decide 113 of the 1534 holdouts.
Cryptids
Several Turing machines have been found that are Cryptids, considered so because each of them have a Collatz-like halting problem, a type of problem that is generally difficult to solve. However, probabilistic arguments have allowed all but one of them to be categorized as probviously halting or probviously non-halting.
Probviously non-halting Cryptids:
1RB1RA_0LC1LE_1LD1LC_1LA0LB_1LF1RE_---0RA(bbch), Antihydra1RB1RC_1LC1LE_1RA1RD_0RF0RE_1LA0LB_---1RA(bbch), a variant of Hydra and Antihydra1RB1LD_1RC1RE_0LA1LB_0LD1LC_1RF0RA_---0RC(bbch), similar to Antihydra1RB0LD_1RC1RF_1LA0RA_0LA0LE_1LD1LA_0RB---(bbch), similar to Antihydra1RB0LB_1LC0RE_1LA1LD_0LC---_0RB0RF_1RE1RB(bbch), similar to Antihydra1RB1LA_1LC0RE_1LF1LD_0RB0LA_1RC1RE_---0LD(bbch)
Probviously halting Cryptids:
1RB0RD_0RC1RE_1RD0LA_1LE1LC_1RF0LD_---0RA(bbch), Lucy's Moonlight1RB1RA_0RC1RC_1LD0LF_0LE1LE_1RA0LB_---0LC(bbch), a family of 16 related TMs1RB1RE_1LC1LD_---1LA_1LB1LE_0RF0RA_1LD1RF(bbch)1RB0RE_1LC1LD_0RA0LD_1LB0LA_1RF1RA_---1LB(bbch)1RB0LC_0LC0RF_1RD1LC_0RA1LE_---0LD_1LF1LA(bbch)1RB0LC_1LC0RD_1LF1LA_1LB1RE_1RB1LE_---0LE(bbch)1RB---_0RC0RE_1RD1RF_1LE0LB_1RC0LD_1RC1RA(bbch)1RB0LD_1RC1RA_1LD0RB_1LE1LA_1RF0RC_---1RE(bbch)1RB1LD_1RC0LE_1LA1RE_0LF1LA_1RB0RB_---0LB(bbch)1RB0RE_1LC0RA_1LA1LD_1LC1LF_0LC0LB_1LE---(bbch)
Although 1RB1LE_0LC0LB_1RD1LC_1RD1RA_1RF0LA_---1RE (bbch) behaves similarly to the probviously halting Cryptids, it is estimated to have a 3/5 chance of becoming a translated cycler and a 2/5 chance of halting.
There are a few machines considered notable for their chaotic behaviour, but which have not been classified as Cryptids due to seemingly lacking a connection to any known open mathematical problems, such as Collatz-like problems.
Potential Cryptids:
1RB1RE_1LC0RA_0RD1LB_---1RC_1LF1RE_0LB0LE(bbch)1RB0LD_1LC0RA_1RA1LB_1LA1LE_1RF0LC_---0RE(bbch)1RB0RB_1LC1RE_1LF0LD_1RA1LD_1RC1RB_---1LC(bbch)1RB0LD_0RC0RE_1LC0LA_---1LE_0LF0RE_0RA0LE(bbch)1RB1RF_1LC1LF_0RE1LD_0LB1LD_---1RC_1RA0RD(bbch)
Top Halters
Below is a table of the machines with the 20 highest known runtimes.[1] Their sigma scores are expressed using an extension of Knuth's up-arrow notation.[2]
| Standard format | (approximate) Σ | Discoverer |
|---|---|---|
1RB1RA_1RC1RZ_1LD0RF_1RA0LE_0LD1RC_1RA0RE (bbch)
|
2 ↑↑↑ 5 | mxdys |
1RB1LC_1LA1RE_0RD0LA_1RZ1LB_1LD0RF_0RD1RB (bbch)
|
10 ↑↑ 11010000 | mxdys |
1RB0LD_1RC0RF_1LC1LA_0LE1RZ_1LF0RB_0RC0RE (bbch)
|
10 ↑↑ 15.60465 | Pavel Kropitz |
1RB0LF_1RC1RB_1LD0RA_1LB0LE_1RZ0LC_1LA1LF (bbch)
|
10 ↑↑ 7.52390 | |
1RB0LF_1RC1RB_1LD0RA_1RF0LE_1RZ0LC_1LA1LF (bbch)
|
10 ↑↑ 7.52390 | |
1RB0LF_1RC1RB_1LD0RA_1LF0LE_1RZ0LC_1LA1LF (bbch)
|
10 ↑↑ 7.52390 | |
1RB1RC_1LC1RE_1LD0LB_1RE1LC_1LE0RF_1RZ1RA (bbch)
|
10 ↑↑ 7.23619 | |
1RB1RA_1LC1LE_1RE0LD_1LC0LF_1RZ0RA_0RA0LB (bbch)
|
10 ↑↑ 6.96745 | poppuncher |
1RB0RF_1LC0RA_1RZ0LD_1LE1LD_1RB1RC_0LD0RE (bbch)
|
10 ↑↑ 5.77573 | poppuncher |
1RB0LA_1LC1LF_0LD0LC_0LE0LB_1RE0RA_1RZ1LD (bbch)
|
10 ↑↑ 5.63534 | Shawn Ligocki |
1RB1RE_1LC1LF_1RD0LB_1LE0RC_1RA0LD_1RZ1LC (bbch)
|
10 ↑↑ 5.56344 | |
1RB0LE_0RC1RA_0LD1RF_1RE0RB_1LA0LC_0RD1RZ (bbch)
|
10 ↑↑ 5.12468 | |
1RB0RF_1LC1LB_0RE0LD_0LC0LB_0RA1RE_0RD1RZ (bbch)
|
10 ↑↑ 5.03230 | |
1RB1LA_1LC0RF_1LD1LC_1LE0RE_0RB0LC_1RZ1RA (bbch)
|
10 ↑↑ 4.91072 | |
1RB0LE_1LC1RA_1RE0LD_1LC1LF_1LA0RC_1RZ1LC (bbch)
|
10 ↑↑ 3.33186 | |
1RB1RF_1LC1RE_0LD1LB_1LA0RA_0RA0RB_1RZ0RD (bbch)
|
10 ↑↑ 3.31128 | |
1RB0LF_1LC0RA_1RD0LB_1LE1RC_1RZ1LA_1LA1LE (bbch)
|
10 ↑↑ 3.18855 | |
1RB0RF_1LC1RB_0RD0LB_1RZ0LE_1RE0RA_1RD1RE (bbch)
|
10 ↑↑ 3.16005 | |
1RB1RZ_0LC0LD_1LD1LC_1RE1LB_1RF1RD_0LD0RA (bbch)
|
Pavel Kropitz | |
1RB0RC_0LC0LB_0LD1LC_0LE1LA_0LF---_1RF1RA (bbch)
|
(lower bound) | Racheline |
The runtimes are presumed to be about which is roughly indistinguishable in tetration notation.
Holdouts
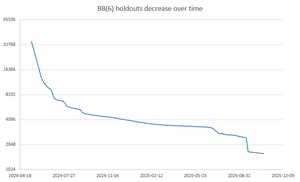
@mxdys's informal holdouts list has 1326 machines up to equivalence as of December 2025. Partial Rocq proof is available on Github.
Always up-to-date annotated spreadsheet, with links to Discord discussions: Spreadsheet.
All holdouts have been simulated up to at least 1e12 steps. 210 holdouts have not been simulated out to 1e13 steps. (The list can be found in the spreadsheet)
References
- ↑ Shawn Ligocki's list of 6-state, 2-symbol machines with large runtimes (Link)
- ↑ Shawn Ligocki. 2022. "Extending Up-arrow Notation"