Unsolved problem: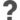
Does Bigfoot run forever?
Bigfoot (1RB2RA1LC_2LC1RB2RB_---2LA1LA (bbch)) is a BB(3,3) Cryptid. Its low-level behaviour was first shared over Discord by savask on 14 Oct 2023, and within two days, Shawn Ligocki described the high-level rules shown below, whose attributes inspired the Turing machine's name.[1]
|
0 |
1 |
2
|
| A
|
1RB
|
2RA
|
1LC
|
| B
|
2LC
|
1RB
|
2RB
|
| C
|
---
|
2LA
|
1LA
|
The transition table of Bigfoot.
In May of 2024, Iijil compiled Bigfoot into a 7-state 2-symbol machine 0RB1RB_1LC0RA_1RE1LF_1LF1RE_0RD1RD_1LG0LG_---1LB (bbch).
Analysis
Let . Then,
Proof
For now, we will work with the slightly different configuration . Consider the partial configuration . We first require the following shift rule:
Using this shift rule, we get after steps, followed by four steps later. Observing that becomes in two steps leads to another shift rule:
From here, there are two different scenarios depending on if is even or odd, given below as histories of transitions that use the aforementioned shift rules:
- If , then what follows is:Therefore, we have
- If , then what follows is:Therefore, we have
From this we know that Bigfoot's behaviour depends on the value of modulo 12, and with we have . The following shift rules will be useful:
Only even values of and are relevant, so there remain six possible scenarios:
- If , then in steps we arrive at , or when considering the complete configuration. What follows is:This means that if , then we will reach in steps.
- If , then in steps we arrive at , or . What follows is:This means that if , then we will reach in steps.
- If , then in steps we arrive at , or . What follows is:This means that if , then Bigfoot will reach the undefined
C0 transition with the configuration in steps. Otherwise, it will proceed to reach in steps.
- If , then in steps we arrive at , or . What follows is:This means that we will reach in steps.
- If , then in steps we arrive at , or . What follows is:This means that we will reach in steps.
- If , then in steps we arrive at , or . What follows is:This means that we will reach in steps.
The information above can be summarized as
Using the definitions of and to transform these rules produces this:
Substituting where is the remainder for each case yields the final result.
Using the floor function, it is possible to describe the behaviour of and using a function that is not defined piecewise:
In effect, the halting problem for Bigfoot is about whether through enough iterations of we encounter more values that are congruent to 2 modulo 6 than ones that are congruent to 1 or 4 modulo 6.
An important insight is that if is odd and , then after four iterations of , that will remain the case. This allows one to define a configuration that eliminates the parameter and whose rules use a modulus of 81.[1]
Trajectory
After 69 steps, Bigfoot will reach the configuration before the Collatz-like rules are repeatedly applied. Simulations of Bigfoot have shown that after 24000000 rule steps, we have . Here are the first few:
There exists a heuristic argument for Bigfoot being probviously non-halting. By only considering the rules for which changes, one may notice that the trajectory of values can be approximated by a random walk in which at each step, the walker moves +1 with probability or moves -1 with probability , starting at position 2. If is the probability that the walker will reach position -1 from position , then . Solutions to this recurrence relation come in the form , which after applying the appropriate boundary conditions reduces to . As a result, if the walker gets to position 3999888, then the probability of it ever reaching position -1 would be .
References