1RB2LC1RC_2LC---2RB_2LA0LB0RA

Unsolved problem:

Does this TM halt? If so, how many steps does it take to halt?

1RB2LC1RC_2LC---2RB_2LA0LB0RA (bbch) is a BB(3,3) holdout which appears to probviously halt. If it can be proven to halt, it will be the BB(3,3) champion in terms of both steps and tape symbols. However, it could also turn out to be a probviously halting Cryptid.

This is holdout #758 on Justin's 3x3 mugshots. After about 1.8 million steps and up to some relabelling, it is equivalent to holdout #153: 1RB0LB0RC_2LC2LA1RA_1RA1LC--- (bbch). And if you start in state C it is a permutation of the same machine. Together, they simulate a complex set of Collatz-like rules with two decreasing parameters.

After active exploration on the #bb3x3 channel by LegionMammal and dyuan, LegionMammal found (and dyuan confirmed) a configuration A(1,c) (defined here) which halts and for which a huge "wall" of previous A(1, c') values all reach it. This gives strong evidence that the TM probviosly halts since jumping over this wall is very "unlikely".

NOTE: As of 16 Jul 2024 there is a lot more active work on the #bb3x3 channel with LegionMammal and dyuan not reflected here.

dyuan01's Rules

https://discord.com/channels/960643023006490684/1084047886494470185/1224457633176486041

A_1(a, b, c) = 0^inf 1 2^a <C (22)^b (20)^c 0^inf
A_2(a, b, c) = 0^inf 1 2^a <A2 (22)^b (20)^c 0^inf
B(a, b) = 0^inf 1 2^a <B0 (20)^b 0^inf

From	To
A₁(0, b, 2n)	A₂(1, b+2n+1, 0)
A₁(0, b, 2n+1)	A₁(1, 0, b+2n+3)
A₁(m+1, b, 0)	A₁(m, 0, b+2)
A₁(m+1, b, n+1)	A₂(m, b+1, n)
A₂(0, b, 2n)	A₁(2b+3, 0, 2n+1)
A₂(0, b, 2n+1)	A₂(2b+3, 2n+1, 0)
A₂(m+1, b, 0)	B(m, b+2)
A₂(m+1, b, n+1)	A₁(m, b+2, n)
B(0, b)	Halt
B(m+1, 2n)	A₂(m, 2n+1, 0)
B(m+1, 2n+1)	A₁(m, 0, 2n+3)

Starting from A₁(0, 0, 1) (at step 2).

savask's Rules

https://discord.com/channels/960643023006490684/1084047886494470185/1254085725138190336

Let (m, b, n) = A2(m, b, n) = 0^inf 1 2^m <A2 (22)^b (20)^n 0^inf

(0, b, n) -> (2b+2, 1, n) if n is even
          -> (2b, 1, n+3) if n is odd

(1, b, 0) -> Halt

(2, b, 0) -> (0, b+3, 0) if b is even
          -> (0, 1, b+5) if b is odd

(m, b, 0) -> (m-2, b+3, 0) if b is even
          -> (m-3, 1, b+3) if b is odd

(1, b, n) -> (0, 1, n+b+2) if n is even
          -> Halt if n is odd

(2, b, 1) -> Halt if b is even
          -> (0, 1, b+5) if b is odd

(m, b, 1) -> (m-3, 1, b+3)

(m, b, n) -> (m-2, b+3, n-2)

https://discord.com/channels/960643023006490684/1084047886494470185/1254306301786198116

step (A2 0 b n) | even n = A2 (2*b+2) 1 n
                | otherwise = A2 (2*b) 1 (n+3)
-- From now on m > 0
step (A2 1 b 0) = error $ "Halt A2 1 " ++ show b ++ " 0"
step (A2 2 b 0) | even b = A2 0 (b+3) 0
                | otherwise = A2 0 1 (b+5)
step (A2 m b 0) | even b = A2 (m-2) (b+3) 0
                | otherwise = A2 (m-3) 1 (b+3)
-- From now on n > 0
step (A2 1 b n) | even n = A2 0 1 (n+b+2)
                | otherwise = error $ "Halt A2 1 " ++ show b ++ " " ++ show n
step (A2 2 b 1) | even b = error $ "Halt A2 2 " ++ show b ++ " 1"
                | otherwise = A2 0 1 (b+5)
step (A2 m b 1) = A2 (m-3) 1 (b+3)
-- Here m > 1, n > 1
step (A2 m b n) = let d2 = (min m n) `div` 2 in A2 (m - 2*d2) (b + 3*d2) (n - 2*d2) -- Accelerated

Shawn's Rules

https://discord.com/channels/960643023006490684/1084047886494470185/1254307091863048264

We can reduce the set of rules from savask's list a bit by noticing that we can evaluate so that all rules end with c even:

  (0, b, 2c)    -> (2b+2, 1, 2c)

  (1, b, 0) -> Halt
  (1, 2b,   2c)  -> (0, 1, 2(b+c+1))
  (1, 2b+1, 2c)  -> (2, 1, 2(b+c+3))

  (a, 2b,   0)  -> (a-2, 2b+3, 0)
  (2, 2b+1, 0)  -> (0, 1, 2b+6)
  (a, 2b+1, 0)  -> (a-3, 1, 2b+4)

  (a, b, c) -> (a-2, b+3, c-2)

Phases

We can think of this going through two different phases. "Even Phase" (where a is even) and "Odd Phase" (where a is odd).

Even Phase: a,c even:
  (0, b, 2c) -> (2b+2, 1, 2c)
  (2a+2, 2b, 0) -> (2a, 2b+3, 0)
  (2, 2b+1, 0) -> (0, 1, 2(b+3))

  To Odd Phase:
    (2a+4, 2b+1, 0) -> (2a+1, 1, 2b+4)
 
Odd Phase: a odd, c even
  To Halt:
    (1, b, 0) -> Halt
    (3, 2b, 0) -> (1, 2b+3, 0) -> Halt

  To Even Phase:
    (1, 2b, 2c+2) -> (0, 1, 2(b+c+2))
    (1, 2b+1, 2c+2) -> (0, 1, 2b+2c+5) -> (2, 1, 2(b+c+4))
    
    (2a+5, 2b, 0) -> (2a+3, 2b+3, 0) -> (2a, 1, 2b+6)
    (2a+3, 2b+1, 0)  -> (2a, 1, 2b+4)

So the only way for this to halt is if it is in "Even Phase" and hits (2k+8, 2k+1, 0) or (4k+12, 4k+3, 0) (which will lead to (1, b, 0) or (3, 2b, 0) eventually). If a is bigger or smaller, then "Odd Phase" will end going back to "Even Phase" again.

Repeated (0, b, 2c)

Let $f (n) = 3 n + 4$ , then $(0, b, 2 c) \to (0, f (b), 2 (c - b - 1))$ Let $h (n) = f^{n} (1) + 1 = 3^{n + 1} - 1$ $g (n) = \sum_{k = 0}^{n - 1} h (k) = \frac{3}{2} (3^{n} - 1) - n$

Then if $c > g (n)$ : $(0, 1, 2 c) \to (0, f^{n} (1), 2 (c - g (n))) \to (2 h (n), 1, 2 (c - g (n)))$

Repeated (0, 1, 2c)

https://discord.com/channels/960643023006490684/1084047886494470185/1254635277020954705

Let $C (n) = (0, 1, 2 n)$ = 0^inf 1 <A2 22 (20)^2n 0^inf

$C (g (n) + 8 k + 1) \to C (g (n) + 8 k + 1 + n + 9)$ $\forall k : \frac{h (n) - 45}{65} < k < \frac{h (n) - 22}{38}$

Notably, when 8 divides (n+1) then this rule can potentially be applied repeatedly.

Ex: if n = 7, then we get: $\forall k \in [101, 172] : C (3273 + 8 k) \to C (3273 + 8 (k + 2))$

And we see this starting with $C (4137) = C (3273 + 8 \cdot 108)$ which repeats this rule until we get to $C (4665) = C (3273 + 8 \cdot 174)$ .

And as n gets way bigger, these ranges of repeat will increase exponentially.

A(a, c) Rules and Timings

Let A(a, c) = A₁(a, 0, c) = 0^∞ 1 2^a <C (20)^c 0^∞, where A₁(a, b, c) comes from dyuan01's rules. Then the TM satisfies the following rules once it reaches A(0, 1) after 2 steps. Note that rules (a) and (g) aren't actually reachable from the initial condition.

Rules and associated step counts (source)
	A(a, c) →	Conditions	Step count
(a)	A(a−c−1, 3c/2+2)	c ≤ a−1, c ≡ 0 (mod 2)	3c²+8c+5
(b)	A(a−c−2, 3(c−1)/2+5)	c ≤ a−2, c ≡ 1 (mod 4)	(6c²+31c+37)/2
(c)	A(a−c−4, 3(c−1)/2+8)	c ≤ a−4, c ≡ 3 (mod 4)	3c²+29c+65
(d)	Halt(3(c−1)/2+7)	c = a−3, c ≡ 3 (mod 4)	(6c²+43c+75)/2
(e)	A(3c+8, 1)	c = a−2, c ≡ 3 (mod 4)	(6c²+37c+63)/2
(f)	Halt(3(c−1)/2+4)	c = a−1, c ≡ 1 (mod 2)	3c²+8c+6
(g)	Halt(a/2+c+4)	c ≥ a, a ≡ 0, c ≡ 0 (mod 2)	3a²+5a+9c+24
(h)	A(1, a/2+c+2)	c ≥ a, a ≡ 0, c ≡ 1 (mod 2)	3a²+3a+5c+11
(i)	A(3a, c−a+4)	c ≥ a, a ≡ 1, c ≡ 0 (mod 2)	3a²−9a+14c+30
(j)	A(3a+2, c−a+1)	c ≥ a, a ≡ 1, c ≡ 1 (mod 2)	3a²+5c+6

Large-scale behavior

Consider the behavior of this machine starting at A(0, 1). If we start a new line every time rule (h) is applied, we find that it follows chains of steps, each starting from a config of form A(1, c):

    A(0,1)
-h> A(1,3) -j> A(5,3) -e> A(17,1) -b> A(14,5)
    -b> A(7,11) -j> A(23,5) -b> A(16,11) -c> A(1,23)
    -j> A(5,23) -j> A(17,19) -j> A(53,3) -c> A(46,11)
    -c> A(31,23) -c> A(4,41)
-h> A(1,45) -j> A(5,45) -j> A(17,41) -j> A(53,25)
    -b> A(26,41)
-h> A(1,56) -i> A(3,59) -j> A(11,57) -j> A(35,47)
    -j> A(107,13) -b> A(92,23) -c> A(65,41) -b> A(22,65)
-h> A(1,78) -i> A(3,81) -j> A(11,79) -j> A(35,69)
    -j> A(107,35) -c> A(68,59) -c> A(5,95) -j> A(17,91)
    -j> A(53,75) -j> A(161,23) -c> A(134,41) -b> A(91,65)
    -b> A(24,101)
-h> A(1,115) -j> A(5,115) -j> A(17,111) -j> A(53,95)
    -j> A(161,43) -c> A(114,71) -c> A(39,113) -j> A(119,75)
    -c> A(40,119)
-h> A(1,141) -j> A(5,141) -j> A(17,137) -j> A(53,121)
    -j> A(161,69) -b> A(90,107)
-h> A(1,154) -i> ...

If we look at the sequence of applied rule labels, we can see the overall structure of these chains:

A(0,1) h
A(1,3) jebbjbcjjjccch
A(1,45) jjjbh
A(1,56) ijjjbcbh
A(1,78) ijjjccjjjcbbh
A(1,115) jjjjccjch
A(1,141) jjjjbh
A(1,154) ijjjjbccbbbjch
A(1,194) ijjjjbcbh
A(1,218) ijjjjbcjccbcjbcbbjjjcbjcbch
A(1,298) ijjjjbh
A(1,315) jjjjjccch
A(1,341) jjjjjbcjcbbbjch
A(1,381) jjjjjbcjbh
A(1,405) jjjjjbcjjbh
A(1,431) jjjjjch
A(1,448) ijjjjch
A(1,467) jjjjjch
A(1,484) ijjjjjbcbbbcch
A(1,524) ijjjjjbcccch
A(1,561) jjjjjbh
A(1,576) ijjjjjbbbcjjcbjjbcjbbjch
A(1,640) ijjjjjbbbh
A(1,664) ijjjjjbbch
A(1,690) ijjjjjccjbccbjccch

Following a possible (i) and an initial run of (j), the chain alternates between runs of (b)/(c) and runs of (j). Each run of (b)/(c) is of even length, except for the final run which is of odd length. Starting from A(1, c), the length of the initial run of (j) approaches (log₃ c − 1). Rules (d), (f), and (h) can only occur after an odd-length run of (b)/(c), while rule (e) can only occur after an even-length run.

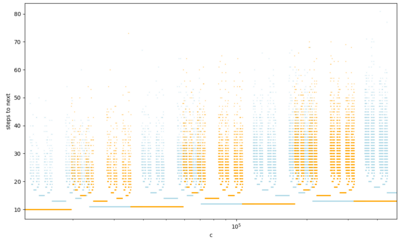
Notice how in the sequence of A(1, c) configs, the next c value is always greater than the previous c value, but not extraordinarily greater. In fact, the difference Δc over the course of a chain is roughly proportional to the length of the chain. We can see this if we reparameterize the rules in terms of t = a+2c and d = (c−1)/2, with the invariant that 0 ≤ d ≤ (t−2)/4 at all times (T(t,d) = A(t-4d-2, 2d+1)):

Rules for T(t, d)
	T(t, d) →	Conditions
(b)	T(t+5, 3d/2+2)	6d ≤ t−5, d ≡ 0 (mod 2)
(c)	T(t+9, 3(d−1)/2+5)	6d ≤ t−7, d ≡ 1 (mod 2)
(d)	Halt(3d+7)	6d = t−6, d ≡ 1 (mod 2)
(e)	T(t+8, 0)	6d = t−5, d ≡ 1 (mod 2)
(f)	Halt(3d+4)	6d = t−4
(h)	T(t+5, (t−2)/4+1)	6d ≥ t−2, t ≡ 2 (mod 4)
(hi)	T(t+13, t/4+2)	6d ≥ t−2, t ≡ 0 (mod 4)
(j)	T(t+4, 3d−(t−1)/2+1)	6d ≥ t−3, t ≡ 1 (mod 2)

In this form, each step increases t by a small positive value, so this explains why Δc between A(1, c) configs depends on the number of steps in the chain.

What determines the number of steps in the chain? As the plot shows, the chain lengths follow a sort of fractal pattern depending on the magnitude of c. To derive this pattern, we first start with our T(t, d) parameterization, combine steps so that t is always odd, and let u = (t−1)/2, so that 0 ≤ d ≤ (u−1)/2. Looking at rules (b), (c), and (j), we find (U(u,d) = T(2u+1, d)):

Rules for U(u, d)
	U(u, d) →	Conditions
(bb)	U(u+5, (9d+20)/4)	0 ≤ d ≤ (2u−12)/9, d ≡ 0 (mod 4)
(cc)	U(u+9, (9d+35)/4)	0 ≤ d ≤ (2u−19)/9, d ≡ 1 (mod 4)
(bc)	U(u+7, (9d+26)/4)	0 ≤ d ≤ (2u−12)/9, d ≡ 2 (mod 4)
(cb)	U(u+7, (9d+29)/4)	0 ≤ d ≤ (2u−17)/9, d ≡ 3 (mod 4)
(j)	U(u+2, 3d−u+1)	(u−1)/3 ≤ d ≤ (u−1)/2

Broadly, it maps d → 9d/4 when 0 < d < 2u/9; hits rule (h) and resets when 2u/9 < d < u/3; and maps d → 3d−u when u/3 < d < u/2. These three subcases form an iterated function system describing a fractal pattern analogous to the ternary Cantor set. The machine checks which interval the ratio 2d/u lies in: if it lies in the middle interval, rule (h) applies, but if it lies in the left or right interval, rules (b), (c), (j) expand its position within that interval, then recursively repeat the check. Similarly to the Cantor set, the fractal has Lebesgue measure 0, so almost all initial points should eventually hit rule (h). As a corollary, the number of steps after the initial (j) run should follow a geometric distribution, so the expected chain length should approach log₃ c plus a constant.

The machine halts if the chain ends at rules (d) or (f), which reside at the right edge of the left intervals within the fractal. Certain configs A(1, c) hit one of these rules before hitting rule (h), and these values of c are called halting values. The first few halting values are:

A(1,12)   -> Halt(40)   via ijjccjcd
A(1,14)   -> Halt(40)   via ijjbcjcd
A(1,71)   -> Halt(100)  via jjjebbccbf
A(1,73)   -> Halt(100)  via jjjjbbccbf
A(1,131)  -> Halt(148)  via jjjjcd
A(1,133)  -> Halt(148)  via jjjjbd
A(1,2331) -> Halt(2377) via jjjjjjjcbccccjbf
A(1,2333) -> Halt(2377) via jjjjjjjbbccccjbf
A(1,2583) -> Halt(2620) via jjjjjjjccbcjbf
A(1,2585) -> Halt(2620) via jjjjjjjbcbcjbf

As a rule, halting values always come in pairs with a difference of 2, except in the unlikely case that a chain hits rule (e) before halting. They are common for small values of c, but soon become exponentially rare. In fact, there only exist 64 total halting values up to c = 3.4×10¹⁵, and the first 58 are known not to be reached by the forward iteration.

First 64 halting values

1. A(1,12) -> Halt(40) via ijjccjcd
2. A(1,14) -> Halt(40) via ijjbcjcd
3. A(1,71) -> Halt(100) via jjjebbccbf
4. A(1,73) -> Halt(100) via jjjjbbccbf
5. A(1,131) -> Halt(148) via jjjjcd
6. A(1,133) -> Halt(148) via jjjjbd
7. A(1,2331) -> Halt(2377) via jjjjjjjcbccccjbf
8. A(1,2333) -> Halt(2377) via jjjjjjjbbccccjbf
9. A(1,2583) -> Halt(2620) via jjjjjjjccbcjbf
10. A(1,2585) -> Halt(2620) via jjjjjjjbcbcjbf
11. A(1,3195) -> Halt(3241) via jjjjjjjcbjbbccjcf
12. A(1,3197) -> Halt(3241) via jjjjjjjbbjbbccjcf
13. A(1,6306) -> Halt(6358) via ijjjjjjjcbjcccbcd
14. A(1,6308) -> Halt(6358) via ijjjjjjjbbjcccbcd
15. A(1,7167) -> Halt(7204) via jjjjjjjjcbcbbd
16. A(1,7169) -> Halt(7204) via jjjjjjjjbbcbbd
17. A(1,11787) -> Halt(11812) via jjjjjjjjcd
18. A(1,11789) -> Halt(11812) via jjjjjjjjbd
19. A(1,13624) -> Halt(13672) via ijjjjjjjjccbbbccf
20. A(1,13626) -> Halt(13672) via ijjjjjjjjbcbbbccf
21. A(1,43122) -> Halt(43165) via ijjjjjjjjjcccbbf
22. A(1,43124) -> Halt(43165) via ijjjjjjjjjbccbbf
23. A(1,905235) -> Halt(905284) via jjjjjjjjjjjjccjjbbjbf
24. A(1,905237) -> Halt(905284) via jjjjjjjjjjjjbcjjbbjbf
25. A(1,956563) -> Halt(956596) via jjjjjjjjjjjjcd
26. A(1,956565) -> Halt(956596) via jjjjjjjjjjjjbd
27. A(1,1712679) -> Halt(1712746) via jjjjjjjjjjjjjcbcbbcjccjcf
28. A(1,1712681) -> Halt(1712746) via jjjjjjjjjjjjjbbcbbcjccjcf
29. A(1,49818027) -> Halt(49818118) via jjjjjjjjjjjjjjjjccbbjbcccccjcbcd
30. A(1,49818029) -> Halt(49818118) via jjjjjjjjjjjjjjjjbcbbjbcccccjcbcd
31. A(1,77484059) -> Halt(77484100) via jjjjjjjjjjjjjjjjcd
32. A(1,77484061) -> Halt(77484100) via jjjjjjjjjjjjjjjjbd
33. A(1,106744976) -> Halt(106745041) via ijjjjjjjjjjjjjjjjccccjjjbf
34. A(1,106744978) -> Halt(106745041) via ijjjjjjjjjjjjjjjjbcccjjjbf
35. A(1,659939159) -> Halt(659939224) via jjjjjjjjjjjjjjjjjjccjjcbjbd
36. A(1,659939161) -> Halt(659939224) via jjjjjjjjjjjjjjjjjjbcjjcbjbd
37. A(1,3822354579) -> Halt(3822354640) via jjjjjjjjjjjjjjjjjjjjccbbcf
38. A(1,3822354581) -> Halt(3822354640) via jjjjjjjjjjjjjjjjjjjjbcbbcf
39. A(1,6276211875) -> Halt(6276211924) via jjjjjjjjjjjjjjjjjjjjcd
40. A(1,6276211877) -> Halt(6276211924) via jjjjjjjjjjjjjjjjjjjjbd
41. A(1,16380092275) -> Halt(16380092362) via jjjjjjjjjjjjjjjjjjjjjccjcbjjjjbbbbcd
42. A(1,16380092277) -> Halt(16380092362) via jjjjjjjjjjjjjjjjjjjjjbcjcbjjjjbbbbcd
43. A(1,404671372119) -> Halt(404671372210) via jjjjjjjjjjjjjjjjjjjjjjjjcbjcccccccf
44. A(1,404671372121) -> Halt(404671372210) via jjjjjjjjjjjjjjjjjjjjjjjjbbjcccccccf
45. A(1,508373165611) -> Halt(508373165668) via jjjjjjjjjjjjjjjjjjjjjjjjcd
46. A(1,508373165613) -> Halt(508373165668) via jjjjjjjjjjjjjjjjjjjjjjjjbd
47. A(1,3957690125931) -> Halt(3957690126046) via jjjjjjjjjjjjjjjjjjjjjjjjjjcbjcbjjccjjcbbbbcjcd
48. A(1,3957690125933) -> Halt(3957690126046) via jjjjjjjjjjjjjjjjjjjjjjjjjjbbjcbjjccjjcbbbbcjcd
49. A(1,4444131579443) -> Halt(4444131579553) via jjjjjjjjjjjjjjjjjjjjjjjjjjcbjjjbbbcbbbbccbccf
50. A(1,4444131579445) -> Halt(4444131579553) via jjjjjjjjjjjjjjjjjjjjjjjjjjbbjjjbbbcbbbbccbccf
51. A(1,8359489573703) -> Halt(8359489573780) via jjjjjjjjjjjjjjjjjjjjjjjjjjjcccbbd
52. A(1,8359489573705) -> Halt(8359489573780) via jjjjjjjjjjjjjjjjjjjjjjjjjjjbccbbd
53. A(1,26358811020231) -> Halt(26358811020352) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjcbcbjcbcbbccbbcbcjbf
54. A(1,26358811020233) -> Halt(26358811020352) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjbbcbjcbcbbccbbcbcjbf
55. A(1,41178226418867) -> Halt(41178226418932) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjcd
56. A(1,41178226418869) -> Halt(41178226418932) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjbd
57. A(1,81795441578679) -> Halt(81795441578764) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjcbccjcd
58. A(1,81795441578681) -> Halt(81795441578764) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjbbccjcd
59. A(1,1326438094216110) -> Halt(1326438094216285) via ijjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjccbcbbjccjcbjcbjccbbcccccccccf
60. A(1,1326438094216112) -> Halt(1326438094216285) via ijjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjbcbcbbjccjcbjcbjccbbcccccccccf
61. A(1,2031355966425479) -> Halt(2031355966425562) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjcbbcbf
62. A(1,2031355966425481) -> Halt(2031355966425562) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjbbbcbf
63. A(1,3335436339933243) -> Halt(3335436339933316) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjcd
64. A(1,3335436339933245) -> Halt(3335436339933316) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjbd

To determine which halting c values should get reached by the forward iteration, we can employ a form of backward reasoning. By the nature of this machine, Δc depends on both the initial (j) run length and the chain length following the run. For longer chains, the length is effectively pseudorandom, so any two sequences of A(1, c) values should eventually hit each other, after which they will have the same values.

If we can find a sufficiently long stretch of consecutive A(1, c) configs that all reach the same halting value, we know that any sequence that reaches that stretch will halt. Conversely, if we find a sufficiently long stretch of A(1, c) configs that skip past a halting value, we know that any sequence that reaches that stretch will skip past the halting value. In the first case, we say that the halting value explodes in terms of how many A(1, c) configs can reach it; in the second case, we say that the halting value dies out.

The first and currently only known halting value that does not die out is H = (3³⁰⁷−8282708212)/13959275. It it reachable from a very long stretch of consecutive A(1, c) configs up to c ≤ H−3,403,055. The lower bound of this stretch is not known, but it goes at least to H-8,000,000 ≤ c thus this stretch is well over 4 million long. Thus, assuming the forward iteration reaches this very long stretch, it will halt at A(1, H), unless it has already reached some earlier halting value.

However, we cannot prove that the forward iteration reaches this long stretch instead of skipping past it. Statistically, the expectation is that Δc = log₃ c + O(1), but we cannot place any easy bound on how long the chain can become: in principle, there could be an undiscovered A(1, c) config that goes on for 10¹⁰⁰⁰ steps or more. So if we want to fully prove that this machine halts at or before A(1, H), we must place an upper bound on Δc for every step leading up to it. But given the size of H, there is no known practical method to compute such an upper bound.

Equivalence to 1RB0LB0RC_2LC2LA1RA_1RA1LC---

1RB0LB0RC_2LC2LA1RA_1RA1LC--- (bbch), #153, eventually becomes equivalent to this machine. As found by @Legion, after running the #153 machine for 1,790,901 steps, if one permutes the states A,C, and B and exchanges 1 for 2 and L for R, it has the same configuration as TM #758 after it has run 1,841,608 steps.

History

LegionMammal's rough timeline of this TM on 30 Apr 2025 (Discord link):

The machine (and its sibling) pass straight through various rounds of cleverly-written deciders
dyuan posts his set of rules and looks into it a bit, Justin notes that he'd briefly looked at it some time back
Shawn and savask write up some acceleration schemes, find empirical evidence that it repeatedly comes close to halting, and speculate that it may actually halt after some period of time
I take a crack at it myself, this time in terms of chains starting from A(1,c) configs, find some c values leading to a halt (showing that there's no obvious structural barrier), and conjecture some heuristics for how long it should take to reach such a halting c value
dyuan and I nail down the ideas of 'halter families' (collections of infinitely many halting c values so we don't have to brute-force them) and 'reachability analysis' (obtaining a strong probvious guess of whether a c value will or won't occur in the machine's actual forward behavior, assuming it hasn't halted beforehand)
dyuan and I race to find a halting c value that 'explodes' (passes the reachability analysis), first within the 'trivial' halter family to no avail, then within all halter families (writing a program to enumerate halter families is extremely fiddly, at this point I treat some of my own code as a black box not to be touched)
By dint of a somewhat more performant program, I find (and dyuan confirms) the $c = \frac{3^{307} - 8 282 708 212}{13 959 275}$ we all know and love, probviously sealing the machine's fate

1RB2LC1RC_2LC---2RB_2LA0LB0RA

Contents

dyuan01's Rules

savask's Rules

Shawn's Rules

Phases

Repeated (0, b, 2c)

Repeated (0, 1, 2c)

A(a, c) Rules and Timings

Large-scale behavior

Equivalence to 1RB0LB0RC_2LC2LA1RA_1RA1LC---

History

Navigation menu

1RB2LC1RC_2LC---2RB_2LA0LB0RA

dyuan01's Rules

savask's Rules

Shawn's Rules

Phases

Repeated (0, b, 2c)

Repeated (0, 1, 2c)

A(a, c) Rules and Timings

Large-scale behavior

Equivalence to 1RB0LB0RC_2LC2LA1RA_1RA1LC---

History

Navigation menu

Search