TMBR: October 2025

Prev: September 2025

This Month in Beaver Research

Next: November 2025

A brave busy beaver confronts the dreaded Antihydra. Copyright Nico Roper. Commissioned for Why Busy Beaver Hunters Fear the Antihydra.

This edition of TMBR is in progress and has not yet been released. Please add any notes you think may be relevant (including in the form a of a TODO with a link to any relevant Discord discussion).

TODO: BB(3x3) month

Wily Coyote, a BB(3,3) holdout

TODO: BB(2x5) month next month (?)

Blog Posts

• 22 Oct 2025. Ben Brubaker. Why Busy Beaver Hunters Fear the Antihydra. (Hacker News thread)

Champions

• Polygon identified a new BB(4,3) champion with a score of over $10{\uparrow }^{4}4$ (1RB1RD1LC_2LB1RB1LC_1RZ1LA1LD_0RB2RA2RD (bbch)). This TM was first proven to halt by Pavel Kropitz in May 2024, but its runtime was not known at the time.
• @zts439 proved that Bug(8,8) = 506. https://discord.com/channels/960643023006490684/1362008236118511758/1423502208422510716

Theory

Piecewise Affine Functions (PAF) were explored as a generalization of the BMO1 rules:

• @Bard proved that 3 dimension PAF are Turing complete.^[1]
• @star proved that 2 dimension PAF are Turing complete.^[2]
• Shawn Ligocki wrote up a proof sketch that 2-region PAF are Turing complete.^[3]
• It was discovered that Amir Ben-Amram had already proven that 2-dim and 2-region PAF were Turing complete in 2015.
• BMO1 is a 2-dim, 2-region PAF so this provides some sense for the difficulty of the problem.
• This introduces a new type of Cryptids separate from previous Collatz-like ones.

Deciders

• Inductive deciders
  • -d rewrote quick_sim.py in C++, achieving a 6-10x faster runtime.^[4][5]
  • Katelyn Douchette is working on an automated inductive decider.^[6][7] (see inductive proofs)

Misc

• @coda shared a mechanical implementation of a Turing Machine, Antihydra.^[8]
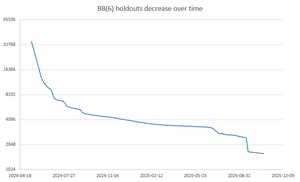
• @Bricks shared a method to estimate susceptibility to Block Analysis and a spreadsheet of BB(6) holdouts quantified by it.^[9][10]

Holdouts

BB(6) Holdouts count decrease overtime.

BB Holdout Reduction by Domain

Domain	New Holdout Count	Previous Holdout Count	Holdout Reduction	% Reduction
BB(6)	1618	1691	73	4.3%
BB(7)	20,405,295	22,801,601	2,396,306	10.5%
BB(4,3)	9,401,447	460,916,384	451,514,937	98.0%
BB(3,4)	15,136,283	434,787,751	419,651,468	96.6%
BB(2,6)	870,085	873,469	3384	0.4%

Details

• BB(6):
  • @mxdys shared a new holdouts list on October 20th, consisting of 1618 machines up to equivalence, or 3067 individual machines. This means 73 newly solved machines, a 4% reduction.
  • @Bricks shared a machine which they thought could be susceptible to block-analysis based on a method they call Subtape Saturation Heuristic. Shawn Ligocki's analysis, simulated by @Bricks showed the machine to halt with a sigma score of 4,419,340,317.
  • Analysis by Racheline showed a machine to be non-halting.
  • mxdys decided a machine from the 50 Random Holdouts introduced back in August, making 10/50 solved.
  • Peacemaker II mentioned a machine which visits only 24 cells after a million steps. mxdys proved the machine nonhalting.
• BB(7):
  • Andrew Ducharme has continued reducing the number of holdouts with Stage 4 of Phase 2. Afterwards, Terry Ligocki ran Stage 5 of Phase 2. Initially, in the beginning of the month there were 22,801,601 holdouts, and 20,405,295 holdouts remain. (10.51% reduction)
• BB(4,3):
  • Terry Ligocki has begun Phase 2 of holdout reduction, reducing the number of holdouts from 460,916,384 to 9,401,447. (97.96% reduction)
• BB(3,4):
  • XnoobSpeakable and Lúkos are running filters in the domain under Phase 2, reducing the holdout count from 434,787,751 to 15,136,283. (96.6% reduction)
• BB(2,5):
  • Peacemaker II gave an informal proof of a machine never halting, making the informal holdout count 64.
• BB(2,6):
  • Andrew Ducharme has completed Stage 3 of Phase 2, reducing the number of holdouts from 873,469 to 870,085. (0.39% reduction)