1RB1LE_1LC0RA_0RF0LD_1LE1LA_1RC0LB_---1RC

Unsolved problem:

Does this TM halt or run forever?

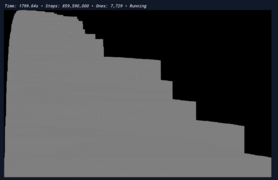
1RB1LE_1LC0RA_0RF0LD_1LE1LA_1RC0LB_---1RC (bbch) is a really interesting BB(6) holdout TM. Wiki user N1vi highly doubts that it halts, but it creates pseudorandom spaces at the right. N1vi also ran it for ~860 million steps and the result is shown in the first image. The machine may be a fractal. @RobinCodes ran it for ~166 billion steps, and the result is shown in the second image.

• 

  The TM ran for ~860 million steps

• 

  The TM ran for ~166 billion steps

-d's Rules

https://discord.com/channels/960643023006490684/1239205785913790465/1411637417709932544

import sys
sys.set_int_max_str_digits(0)

# 1RB1LE_1LC0RA_0RF0LD_1LE1LA_1RC0LB_---1RC
# A(a,b) := 0^inf <C 10^a 110 10^b 0^inf
# B(a,b,c) := 0^inf <C 10^a 110 10^b 110 1010^c 0^inf

# next state for A(a,b), verified up to 0<=a,b<=100 (took ~2 min)
def next_A(a,b):
    if a<b: return (a*2+2,b-a-1)
    if a==b: return ()
    if a>b and (a-b)%2==1: return (a-b+1,b*2+2)
    if a>b and (a-b)%2==0: return (2,a-b-1,b+1)

# next state for B(a,b,c), verified up to 0<=a,b,c<=50 (took ~20 min)
def next_B(a,b,c):
    if a<b: return (a*2+2,b-a-1,c)
    if a==b: return (2,a*4+c*2+6)
    if a>b: return (2,a*2+c*2+2)

s=(2,0)  # start: A(2,0)
for i in range(552187):
    #print(i,s)
    if len(s)==0: break
    elif len(s)==2: s=next_A(*s)
    elif len(s)==3: s=next_B(*s)
    else: assert 0,'not covered'
print('final state',s)

https://discord.com/channels/960643023006490684/1239205785913790465/1413771166555963483

@-d wrote a faster version of this program and ran it until $A(2^{33920}-2,2^{33920}-1154)$. The TM does not halt within $2^{33920}$ steps.