1RB1LE_1LC0RA_0RF0LD_1LE1LA_1RC0LB_---1RC

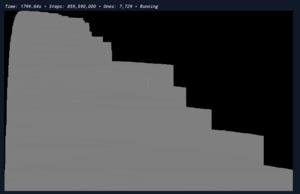
1RB1LE_1LC0RA_0RF0LD_1LE1LA_1RC0LB_---1RC (bbch) is a really interesting BB(6) holdout TM. Wiki user N1vi highly doubts that it halts, but it creates pseudorandom spaces at the right. N1vi also ran it for ~860 million steps and the result is shown in the image. The machine may be a fractal. Robin Rovenszky (RobinCodes) ran it for ~166 billion steps, and the result is shown in the second image.
-d's Rules
https://discord.com/channels/960643023006490684/1239205785913790465/1411637417709932544
import sys
sys.set_int_max_str_digits(0)
# 1RB1LE_1LC0RA_0RF0LD_1LE1LA_1RC0LB_---1RC
# A(a,b) := 0^inf <C 10^a 110 10^b 0^inf
# B(a,b,c) := 0^inf <C 10^a 110 10^b 110 1010^c 0^inf
# next state for A(a,b), verified up to 0<=a,b<=100 (took ~2 min)
def next_A(a,b):
if a<b: return (a*2+2,b-a-1)
if a==b: return ()
if a>b and (a-b)%2==1: return (a-b+1,b*2+2)
if a>b and (a-b)%2==0: return (2,a-b-1,b+1)
# next state for B(a,b,c), verified up to 0<=a,b,c<=50 (took ~20 min)
def next_B(a,b,c):
if a<b: return (a*2+2,b-a-1,c)
if a==b: return (2,a*4+c*2+6)
if a>b: return (2,a*2+c*2+2)
s=(2,0) # start: A(2,0)
for i in range(552187):
#print(i,s)
if len(s)==0: break
elif len(s)==2: s=next_A(*s)
elif len(s)==3: s=next_B(*s)
else: assert 0,'not covered'
print('final state',s)