TMBR: October 2025
| Prev: September 2025 | This Month in Beaver Research | Next: November 2025 |

This Month in Beaver Research for October 2025.
This month we had an eclectic mix of results. We're continuing to see massive holdout reduction at the peripheral domains with a 98% holdout reduction for BB(4,3) while Polygon identified a new BB(4,3) champion. A new type of Cryptid has been explored: Piecewise Affine Functions. Ben Brubaker wrote-up a personal blog post describing Antihydra to a lay audience. @coda designed some physical disks for computing TM transitions. And @-d is developing a C++ version of Quick_Sim.
Blog Posts
- 22 Oct 2025. Ben Brubaker. Why Busy Beaver Hunters Fear the Antihydra. (Hacker News thread)
Champions
- Polygon identified a new BB(4,3) champion with a score of over (
1RB1RD1LC_2LB1RB1LC_1RZ1LA1LD_0RB2RA2RD(bbch)). This TM was first proven to halt by Pavel Kropitz in May 2024, but its runtime was not known at the time. - @Peacemaker II verified the BB(6) champion
1RB1RA_1RC1RZ_1LD0RF_1RA0LE_0LD1RC_1RA0RE(bbch) (and the other members of its "family") and calculated a more precise sigma score of 10↑↑10↑↑10↑↑8.10237 for it.[1] - @zts439 proved that Bug(8,8) = 506.[1]
Theory
Piecewise Affine Functions (PAF) were explored as a generalization of the BMO1 rules:
- @Bard proved that 3 dimension PAF are Turing complete.[1]
- @star proved that 2 dimension PAF are Turing complete.[2][3]
- Shawn Ligocki wrote up a proof sketch that 2-region PAF are Turing complete.[4]
- It was discovered that Amir Ben-Amram had already proven both of these results in 2015 (both the 2-dim and the 2-region results).
- BMO1 is a 2-dim, 2-region PAF so this provides some sense for the difficulty of the problem.
- This introduces a new type of Cryptids separate from previous Collatz-like ones.
Deciders
- Inductive deciders
- @-d is developing a C++ version of Quick_Sim. It can currently solve "Diff Rules" (L1 Inductive Rules). It is 6-10x faster than the original python implementation.[5][6]
- Katelyn Douchette is working on an automated inductive decider.[7][8] (see inductive proofs)
Misc
 |
 |
- @Bricks shared a method to estimate susceptibility to Block Analysis and a spreadsheet of BB(6), BB(3,3) and BB(2,5) holdouts quantified by it.[11][12]
- @Pomme, building onto the work of mxdys, star and Shawn solved BMO #7:
1RB1RF_1RC0RA_1LD1RC_1LE0LE_0RA0LD_0RB---(bbch)[1].
Holdouts
| Domain | New Holdout Count | Previous Holdout Count | Holdout Reduction | % Reduction |
|---|---|---|---|---|
| BB(6) | 1618 | 1691 | 73 | 4.3% |
| BB(7) | 20,405,295 | 22,801,601 | 2,396,306 | 10.5% |
| BB(4,3) | 9,401,447 | 460,916,384 | 451,514,937 | 98.0% |
| BB(3,4) | 15,136,283 | 434,787,751 | 419,651,468 | 96.6% |
| BB(2,6) | 870,085 | 873,469 | 3384 | 0.4% |
Details
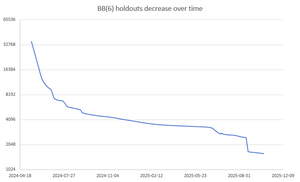
- BB(6):
- @mxdys shared a new holdouts list on October 20th, consisting of 1618 machines up to equivalence, or 3067 individual machines. This means 73 newly solved machines, a 4% reduction.
- @Bricks shared a machine which they thought could be susceptible to block-analysis based on a method they call Subtape Saturation Heuristic. Shawn Ligocki's analysis, simulated by @Bricks showed the machine to halt with a sigma score of 4,419,340,317. Quick_Sim confirmed the result.
- Analysis by Racheline showed a machine to be non-halting.
- mxdys decided a machine from the 50 Random Holdouts introduced back in August, making 10/50 solved.
- Peacemaker II mentioned a machine which visits only 24 cells after a million steps. mxdys proved the machine nonhalting.
- Pomme* solved BMO 7.
- BB(7):
- Andrew Ducharme has continued reducing the number of holdouts with Stage 4 of Phase 2. Afterwards, Terry Ligocki ran Stage 5 of Phase 2. Initially, in the beginning of the month there were 22,801,601 holdouts, and 20,405,295 holdouts remain. (10.51% reduction)
- BB(4,3):
- Terry Ligocki finished Phase 2 of holdout reduction, reducing the number of holdouts from 460,916,384 to 9,401,447. (97.96% reduction)
- BB(3,4):
- XnoobSpeakable and Lúkos are running filters in the domain under Phase 2, reducing the holdout count from 434,787,751 to 15,136,283. (96.6% reduction)
- BB(2,5):
- Peacemaker II gave an informal proof of a machine never halting, making the informal holdout count 64.
- BB(2,6):
- Andrew Ducharme has completed Stage 3 of Phase 2, reducing the number of holdouts from 873,469 to 870,085. (0.39% reduction)