Hydra function

The Hydra function is a Collatz-like function defined as: $H (n) \equiv n + ⌊ \frac{1}{2} n ⌋ = ⌊ \frac{3}{2} n ⌋ = {\begin{cases} \frac{3 n}{2} & if n \equiv 0 (\mod 2), \\ \frac{3 n - 1}{2} & if n \equiv 1 (\mod 2) . \end{cases}$ It is named as such because of its connection to the unsolved halting problems for the Cryptids Hydra and Antihydra. Due to its simplicity, simulations for both of these Turing machines utilize this function instead of what can initially be proven.

Relationship to Hydra and Antihydra

Using the Hydra function, we can obtain simplified rules for Hydra and Antihydra:

Hydra	Antihydra
Let $C_{H} (a, b) : = 0^{\infty} < A 2 0^{3 (a - 2)} 3^{b} 2 0^{\infty}$ : $\begin{array}{lll} 0^{\infty} A > 0^{\infty} & \overset{20}{\to} & C_{H} (3, 0), \\ C_{H} (2 a, 0) & \overset{54 a^{2} - 48 a - 2}{\to} & 0^{\infty} 3^{9 a - 8} 1 A > 2 0^{\infty}, \\ C_{H} (2 a, b + 1) & \overset{54 a^{2} - 39 a - 5}{\to} & C_{H} (3 a, b), \\ C_{H} (2 a + 1, b) & \overset{4 b + 54 a^{2} - 3 a + 4}{\to} & C_{H} (3 a + 1, b + 2) . \end{array}$	Let $A_{H} (a, b) : = 0^{\infty} 1^{a} 0 1^{b - 4} E > 0^{\infty}$ : $\begin{array}{lll} 0^{\infty} A > 0^{\infty} & \overset{11}{\to} & A_{H} (0, 8), \\ A_{H} (a, 2 b) & \overset{2 a + 3 b^{2} - 1}{\to} & A_{H} (a + 2, 3 b), \\ A_{H} (0, 2 b + 1) & \overset{3 b^{2} - 3 b - 7}{\to} & 0^{\infty} < F 110 1^{3 b - 6} 0^{\infty}, \\ A_{H} (a + 1, 2 b + 1) & \overset{3 b^{2} - 7}{\to} & A_{H} (a, 3 b + 1) . \end{array}$

Proof

Recall the high-level rules for Hydra and Antihydra:

Hydra	Antihydra
Let $C (a, b) : = 0^{\infty} < A 2 0^{a} 3^{b} 2 0^{\infty}$ : $\begin{array}{lll} 0^{\infty} A > 0^{\infty} & \overset{20}{\to} & C (3, 0), \\ C (2 a, 0) & \overset{6 a^{2} + 20 a + 4}{\to} & 0^{\infty} 3^{3 a + 1} 1 A > 2 0^{\infty}, \\ C (2 a, b + 1) & \overset{6 a^{2} + 23 a + 10}{\to} & C (3 a + 3, b), \\ C (2 a + 1, b) & \overset{4 b + 6 a^{2} + 23 a + 26}{\to} & C (3 a + 3, b + 2) . \end{array}$	Let $A (a, b) : = 0^{\infty} 1^{a} 0 1^{b} E > 0^{\infty}$ : $\begin{array}{lll} 0^{\infty} A > 0^{\infty} & \overset{11}{\to} & A (0, 4), \\ A (a, 2 b) & \overset{2 a + 3 b^{2} + 12 b + 11}{\to} & A (a + 2, 3 b + 2), \\ A (0, 2 b + 1) & \overset{3 b^{2} + 9 b - 1}{\to} & 0^{\infty} < F 110 1^{3 b} 0^{\infty}, \\ A (a + 1, 2 b + 1) & \overset{3 b^{2} + 12 b + 5}{\to} & A (a, 3 b + 3) . \end{array}$

Already, both machines appear to be very similar. They have one parameter that increases exponentially with growth factor $\frac{3}{2}$ and another that takes a pseudo-random walk. Below, the exponentially increasing variables are described by integer sequences:

Hydra	Antihydra
$a_{0} = 3, a_{n + 1} = {\begin{cases} \frac{3 a_{n} + 6}{2} & if a_{n} \equiv 0 (\mod 2) \\ \frac{3 a_{n} + 3}{2} & if a_{n} \equiv 1 (\mod 2) \end{cases}$	$a_{0} = 4, a_{n + 1} = {\begin{cases} \frac{3 a_{n} + 4}{2} & if a_{n} \equiv 0 (\mod 2) \\ \frac{3 a_{n} + 3}{2} & if a_{n} \equiv 1 (\mod 2) \end{cases}$

This will make demonstrating the transformation easier. Now we will define a new integer sequence based on the old one and discover the recursive rules for that sequence. This new sequence is $b_{n} = \frac{1}{3} a_{n} + 2$ and $b_{n} = a_{n} + 4$ for Hydra and Antihydra respectively. We start by using $b_{n + 1}$ instead and substituting $a_{n + 1}$ for its recursive formula. By doing so, we get:

Hydra	Antihydra
$b_{0} = 3, b_{n + 1} = {\begin{cases} \frac{a_{n} + 6}{2} & if a_{n} \equiv 0 (\mod 2) \\ \frac{a_{n} + 5}{2} & if a_{n} \equiv 1 (\mod 2) \end{cases}$	$b_{0} = 8, b_{n + 1} = {\begin{cases} \frac{3 a_{n} + 12}{2} & if a_{n} \equiv 0 (\mod 2) \\ \frac{3 a_{n} + 11}{2} & if a_{n} \equiv 1 (\mod 2) \end{cases}$

After that, we can substitute $a_{n}$ for its solution in terms of $b_{n}$ . What results is the following:

Hydra	Antihydra
$b_{0} = 3, b_{n + 1} = {\begin{cases} \frac{3 (b_{n} - 2) + 6}{2} & if 3 (b_{n} - 2) \equiv 0 (\mod 2) \\ \frac{3 (b_{n} - 2) + 5}{2} & if 3 (b_{n} - 2) \equiv 1 (\mod 2) \end{cases}$	$b_{0} = 8, b_{n + 1} = {\begin{cases} \frac{3 (b_{n} - 4) + 12}{2} & if b_{n} - 4 \equiv 0 (\mod 2) \\ \frac{3 (b_{n} - 4) + 11}{2} & if b_{n} - 4 \equiv 1 (\mod 2) \end{cases}$

The $if$ statements amount to checking if $b_{n}$ is even or odd. After simplifying, we are done:

Hydra	Antihydra
$b_{0} = 3, b_{n + 1} = {\begin{cases} \frac{3 b_{n}}{2} & if b_{n} \equiv 0 (\mod 2) \\ \frac{3 b_{n} - 1}{2} & if b_{n} \equiv 1 (\mod 2) \end{cases}$	$b_{0} = 8, b_{n + 1} = {\begin{cases} \frac{3 b_{n}}{2} & if b_{n} \equiv 0 (\mod 2) \\ \frac{3 b_{n} - 1}{2} & if b_{n} \equiv 1 (\mod 2) \end{cases}$

Now that we have demonstrated a strong similarity in the behaviour of both Turing machines, we can return to using the high-level rules. Doing that while considering the step counts yields the final result.

Under these rules, the halting problem for Hydra is about whether repeatedly applying the function $H (n)$ , starting with $n = 3$ , will eventually generate more even terms than twice the number of odd terms. Similarly, Antihydra halts if and only if repeatedly applying $H (n)$ , starting with $n = 8$ , will eventually generate more odd terms than twice the number of even terms.

Coding the Hydra function

The Hydra function's simple definition allows one to write computer programs that simulate Hydra and Antihydra. The following Python program is a straightforward Hydra simulator based on the Hydra function:

# 'a' and 'b' fulfill the same purpose as in the Hydra rules.
a = 3
b = 0
# As long as Hydra has not halted, 'b' remains greater than -1.
while b != -1:
    # If 'a' is even, decrement 'b', otherwise increase 'b' by 2.
    if a % 2 == 0:
        b -= 1
    else:
        b += 2
    # This performs H(a) = a + floor(a/2).
    # Note that integer division by 2 is equivalent to one bit shift to the right (a >> 1)
    a += a//2

Replacing a = 3 with a = 8 and swapping b -= 1 with b += 2 turns this program into an Antihydra simulator.

Properties

The Hydra function can be rewritten as follows: $\begin{array}{l} H (2 n) & = & 3 n, \\ H (2 n + 1) & = & 3 n + 1 . \end{array}$ Now assume that for some positive integer $s$ and every odd integer $t$ , $H^{s} (2^{s} t) = 3^{s} t$ and $H^{s} (2^{s} t + 1) = 3^{s} t + 1$ , where $H^{i} (n)$ is function iteration. Notice that we can write $2^{s + 1} t = 2 \cdot 2^{s} t$ and $2^{s + 1} t + 1 = 2 \cdot 2^{s} t + 1$ , so if we apply $H$ to these numbers, we get $H (2 \cdot 2^{s} t) = 3 \cdot 2^{s} t$ and $H (2 \cdot 2^{s} t + 1) = 3 \cdot 2^{s} t + 1$ . Now, if we apply $H$ to these numbers $s$ times, we get $H^{s + 1} (2^{s + 1} t) = H^{s} (2^{s} \cdot 3 t) = 3^{s + 1} t$ and $H^{s + 1} (2^{s + 1} t + 1) = H^{s} (2^{s} \cdot 3 t + 1) = 3^{s + 1} t + 1$ . Therefore, by mathematical induction we have proved the following formulas: $\begin{array}{l} H^{s} (2^{s} t) & = & 3^{s} t, \\ H^{s} (2^{s} t + 1) & = & 3^{s} t + 1 . \end{array}$ This optimization can be directly applied to the high-level rules for Hydra and Antihydra, producing this result:

Hydra	Antihydra
Let $C_{H} (a, b) : = 0^{\infty} < A 2 0^{3 (a - 2)} 3^{b} 2 0^{\infty}$ : $\begin{array}{lll} C_{H} (2^{s} t, b + s) & \overset{f_{1} (s, t)}{\to} & C_{H} (3^{s} t, b), \\ C_{H} (2^{s} t + 1, b) & \overset{f_{2} (s, t, b)}{\to} & C_{H} (3^{s} t + 1, b + 2 s), \end{array}$ where $f_{1} (s, t) = \frac{3 t (3^{s} - 2^{s}) (18 (3^{s} + 2^{s}) t - 65)}{5} - 5 s$ and $f_{2} (s, t, b) = (b + s) 4 s + \frac{3 t (3^{s} - 2^{s}) (18 (3^{s} + 2^{s}) t - 5)}{5}$ .	Let $A_{H} (a, b) : = 0^{\infty} 1^{a} 0 1^{b - 4} E > 0^{\infty}$ : $\begin{array}{lll} A_{H} (a, 2^{s} t) & \overset{f_{3} (s, t, a)}{\to} & A_{H} (a + 2 s, 3^{s} t), \\ A_{H} (a + s, 2^{s} t + 1) & \overset{f_{4} (s, t)}{\to} & A_{H} (a, 3^{s} t + 1), \end{array}$ where $f_{3} (s, t, a) = (2 a - 3 + 2 s) s + \frac{3 t^{2} (9^{s} - 4^{s})}{5}$ and $f_{4} (s, t) = \frac{3 t^{2} (9^{s} - 4^{s})}{5} - 7 s$ .

Visualizations

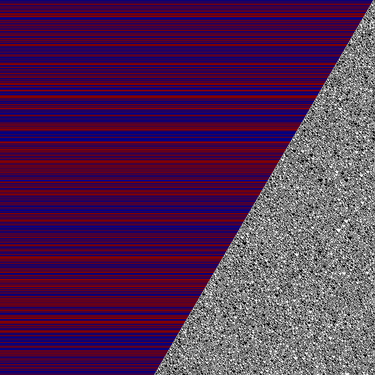
The four images below depict the first 1000 values of four Hydra sequences with different initial values. Each row of pixels shows a number in binary on the right and its parity on the left (blue for even, red for odd):