1RB2LC1RC 2LC---2RB 2LA0LB0RA: Difference between revisions
Added link to Collatz-like |
add explanation |
||
| Line 201: | Line 201: | ||
| A(3a+2, c−a+1) || c ≥ a, a ≡ 1, c ≡ 1 (mod 2) || 3a<sup>2</sup>+5c+6 | | A(3a+2, c−a+1) || c ≥ a, a ≡ 1, c ≡ 1 (mod 2) || 3a<sup>2</sup>+5c+6 | ||
|} | |} | ||
== Large-scale behavior == | |||
Consider the behavior of this machine starting at A(0, 1). If we start a new line every time rule (h) is applied, we find that it follows ''chains'' of steps, each starting from a config of form A(1, ''c''): | |||
A(0,1) | |||
-h> '''A(1,3)''' -j> A(5,3) -e> A(17,1) -b> A(14,5) | |||
-b> A(7,11) -j> A(23,5) -b> A(16,11) -c> A(1,23) | |||
-j> A(5,23) -j> A(17,19) -j> A(53,3) -c> A(46,11) | |||
-c> A(31,23) -c> A(4,41) | |||
-h> '''A(1,45)''' -j> A(5,45) -j> A(17,41) -j> A(53,25) | |||
-b> A(26,41) | |||
-h> '''A(1,56)''' -i> A(3,59) -j> A(11,57) -j> A(35,47) | |||
-j> A(107,13) -b> A(92,23) -c> A(65,41) -b> A(22,65) | |||
-h> '''A(1,78)''' -i> A(3,81) -j> A(11,79) -j> A(35,69) | |||
-j> A(107,35) -c> A(68,59) -c> A(5,95) -j> A(17,91) | |||
-j> A(53,75) -j> A(161,23) -c> A(134,41) -b> A(91,65) | |||
-b> A(24,101) | |||
-h> '''A(1,115)''' -j> A(5,115) -j> A(17,111) -j> A(53,95) | |||
-j> A(161,43) -c> A(114,71) -c> A(39,113) -j> A(119,75) | |||
-c> A(40,119) | |||
-h> '''A(1,141)''' -j> A(5,141) -j> A(17,137) -j> A(53,121) | |||
-j> A(161,69) -b> A(90,107) | |||
-h> '''A(1,154)''' -i> ... | |||
If we look at the sequence of applied rule labels, we can see the overall structure of these chains: | |||
A(0,1) h | |||
A(1,3) jebbjbcjjjccch | |||
A(1,45) jjjbh | |||
A(1,56) ijjjbcbh | |||
A(1,78) ijjjccjjjcbbh | |||
A(1,115) jjjjccjch | |||
A(1,141) jjjjbh | |||
A(1,154) ijjjjbccbbbjch | |||
A(1,194) ijjjjbcbh | |||
A(1,218) ijjjjbcjccbcjbcbbjjjcbjcbch | |||
A(1,298) ijjjjbh | |||
A(1,315) jjjjjccch | |||
A(1,341) jjjjjbcjcbbbjch | |||
A(1,381) jjjjjbcjbh | |||
A(1,405) jjjjjbcjjbh | |||
A(1,431) jjjjjch | |||
A(1,448) ijjjjch | |||
A(1,467) jjjjjch | |||
A(1,484) ijjjjjbcbbbcch | |||
A(1,524) ijjjjjbcccch | |||
A(1,561) jjjjjbh | |||
A(1,576) ijjjjjbbbcjjcbjjbcjbbjch | |||
A(1,640) ijjjjjbbbh | |||
A(1,664) ijjjjjbbch | |||
A(1,690) ijjjjjccjbccbjccch | |||
Following a possible (i) and an initial run of (j), the chain alternates between runs of (b)/(c) and runs of (j). Each run of (b)/(c) is of even length, except for the final run which is of odd length. Starting from A(1, ''c''), the length of the initial run of (j) approaches (log<sub>3</sub> ''c'' − 1). Rules (d), (f), and (h) can only occur after an odd-length run of (b)/(c), while rule (e) can only occur after an even-length run. | |||
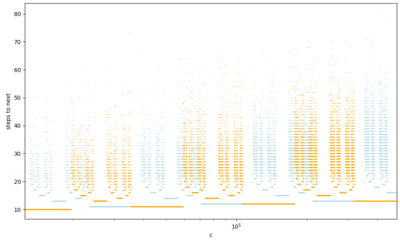
[[File:758 chain lengths.png|thumb|400px|right|alt=A 2D plot of blue and orange points. The values are organized into branching trees of intervals that become progressively smaller until they turn into scattered clouds of points.|Chain lengths starting at A(1, ''c'') configs. Blue points correspond to ''c'' odd, orange points to ''c'' even. The log scale for ''c'' illustrates the recursive structure.]] | |||
Notice how in the sequence of A(1, ''c'') configs, the next ''c'' value is always greater than the previous ''c'' value, but not extraordinarily greater. In fact, the difference Δ''c'' over the course of a chain is roughly proportional to the length of the chain. We can see this if we reparameterize the rules in terms of ''t'' = ''a''+2''c'' and ''d'' = (''c''−1)/2, with the invariant that 0 ≤ ''d'' ≤ (''t''−2)/4 at all times: | |||
{| class="wikitable" style="text-align:left" | |||
|+ Rules for T(t, d) | |||
! !! style="text-align:left" | T(t, d) → !! Conditions | |||
|- | |||
! style="text-align:right" | (b) | |||
| T(t+5, 3d/2+2) || 6d ≤ t−5, d ≡ 0 (mod 2) | |||
|- | |||
! style="text-align:right" | (c) | |||
| T(t+9, 3(d−1)/2+5) || 6d ≤ t−7, d ≡ 1 (mod 2) | |||
|- | |||
! style="text-align:right" | (d) | |||
| Halt(3d+7) || 6d = t−6, d ≡ 1 (mod 2) | |||
|- | |||
! style="text-align:right" | (e) | |||
| T(t+8, 0) || 6d = t−5, d ≡ 1 (mod 2) | |||
|- | |||
! style="text-align:right" | (f) | |||
| Halt(3d+4) || 6d = t−4 | |||
|- | |||
! style="text-align:right" | (h) | |||
| T(t+5, (t−2)/4+1) || 6d ≥ t−2, t ≡ 2 (mod 4) | |||
|- | |||
! style="text-align:right" | (hi) | |||
| T(t+13, t/4+2) || 6d ≥ t−2, t ≡ 0 (mod 4) | |||
|- | |||
! style="text-align:right" | (j) | |||
| T(t+4, 3d−(t−1)/2+1) || 6d ≥ t−3, t ≡ 1 (mod 2) | |||
|} | |||
In this form, each step increases ''t'' by a small positive value, so this explains why Δ''c'' between A(1, ''c'') configs depends on the number of steps in the chain. | |||
What determines the number of steps in the chain? As the plot shows, the chain lengths follow a sort of fractal pattern depending on the magnitude of ''c''. To derive this pattern, we first start with our T(''t'', ''d'') parameterization, combine steps so that ''t'' is always odd, and let ''u'' = (''t''−1)/2, so that 0 ≤ ''d'' ≤ (''u''−1)/2. Looking at rules (b), (c), and (j), we find: | |||
{| class="wikitable" style="text-align:left" | |||
|+ Rules for U(u, d) | |||
! !! style="text-align:left" | U(u, d) → !! Conditions | |||
|- | |||
! style="text-align:right" | (bb) | |||
| U(u+5, (9d+20)/4) || 0 ≤ d ≤ (2u−12)/9, d ≡ 0 (mod 4) | |||
|- | |||
! style="text-align:right" | (cc) | |||
| U(u+9, (9d+35)/4) || 0 ≤ d ≤ (2u−19)/9, d ≡ 1 (mod 4) | |||
|- | |||
! style="text-align:right" | (bc) | |||
| U(u+7, (9d+26)/4) || 0 ≤ d ≤ (2u−12)/9, d ≡ 2 (mod 4) | |||
|- | |||
! style="text-align:right" | (cb) | |||
| U(u+7, (9d+29)/4) || 0 ≤ d ≤ (2u−17)/9, d ≡ 3 (mod 4) | |||
|- | |||
! style="text-align:right" | (j) | |||
| U(u+2, 3d−u+1) || (u−1)/3 ≤ d ≤ (u−1)/2 | |||
|} | |||
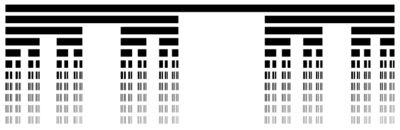
[[File:758 fractal.png|thumb|400px|right|alt=A fractal pattern similar to the ternary Cantor set. A single line appears at the top, followed by 2 shorter lines below it, followed by 4 even shorter lines below those, and so on recursively.|The fractal pattern followed by rules (b), (c), (j). The depth of a given point corresponds to the number of steps before hitting rule (h).]] | |||
Broadly, it maps ''d'' → 9''d''/4 when 0 < ''d'' < 2''u''/9; hits rule (h) and resets when 2''u''/9 < ''d'' < ''u''/3; and maps ''d'' → 3''d''−''u'' when ''u''/3 < ''d'' < ''u''/2. These three subcases form an [[wikipedia:iterated function system|iterated function system]] describing a fractal pattern analogous to the ternary Cantor set. The machine checks which interval the ratio 2''d''/''u'' lies in: if it lies in the middle interval, rule (h) applies, but if it lies in the left or right interval, rules (b), (c), (j) expand its position within that interval, then recursively repeat the check. Similarly to the Cantor set, the fractal has Lebesgue measure 0, so almost all initial points should eventually hit rule (h). As a corollary, the number of steps after the initial (j) run should follow a geometric distribution, so the expected chain length should approach log<sub>3</sub> ''c'' plus a constant. | |||
The machine halts if the chain ends at rules (d) or (f), which reside at the right edge of the left intervals within the fractal. Certain configs A(1, ''c'') hit one of these rules before hitting rule (h), and these values of ''c'' are called ''halting values''. The first few halting values are: | |||
A(1,12) -> Halt(40) via ijjccjcd | |||
A(1,14) -> Halt(40) via ijjbcjcd | |||
A(1,71) -> Halt(100) via jjjebbccbf | |||
A(1,73) -> Halt(100) via jjjjbbccbf | |||
A(1,131) -> Halt(148) via jjjjcd | |||
A(1,133) -> Halt(148) via jjjjbd | |||
A(1,2331) -> Halt(2377) via jjjjjjjcbccccjbf | |||
A(1,2333) -> Halt(2377) via jjjjjjjbbccccjbf | |||
A(1,2583) -> Halt(2620) via jjjjjjjccbcjbf | |||
A(1,2585) -> Halt(2620) via jjjjjjjbcbcjbf | |||
As a rule, halting values always come in pairs with a difference of 2, except in the unlikely case that a chain hits rule (e) before halting. They are common for small values of ''c'', but soon become exponentially rare. In fact, there only exist 64 total halting values up to ''c'' = 3.4×10<sup>15</sup>, and the first 58 are known not to be reached by the forward iteration. | |||
<div class="toccolours mw-collapsible mw-collapsed">'''First 64 halting values'''<div class="mw-collapsible-content"><pre style="overflow:scroll;white-space:pre"> | |||
1. A(1,12) -> Halt(40) via ijjccjcd | |||
2. A(1,14) -> Halt(40) via ijjbcjcd | |||
3. A(1,71) -> Halt(100) via jjjebbccbf | |||
4. A(1,73) -> Halt(100) via jjjjbbccbf | |||
5. A(1,131) -> Halt(148) via jjjjcd | |||
6. A(1,133) -> Halt(148) via jjjjbd | |||
7. A(1,2331) -> Halt(2377) via jjjjjjjcbccccjbf | |||
8. A(1,2333) -> Halt(2377) via jjjjjjjbbccccjbf | |||
9. A(1,2583) -> Halt(2620) via jjjjjjjccbcjbf | |||
10. A(1,2585) -> Halt(2620) via jjjjjjjbcbcjbf | |||
11. A(1,3195) -> Halt(3241) via jjjjjjjcbjbbccjcf | |||
12. A(1,3197) -> Halt(3241) via jjjjjjjbbjbbccjcf | |||
13. A(1,6306) -> Halt(6358) via ijjjjjjjcbjcccbcd | |||
14. A(1,6308) -> Halt(6358) via ijjjjjjjbbjcccbcd | |||
15. A(1,7167) -> Halt(7204) via jjjjjjjjcbcbbd | |||
16. A(1,7169) -> Halt(7204) via jjjjjjjjbbcbbd | |||
17. A(1,11787) -> Halt(11812) via jjjjjjjjcd | |||
18. A(1,11789) -> Halt(11812) via jjjjjjjjbd | |||
19. A(1,13624) -> Halt(13672) via ijjjjjjjjccbbbccf | |||
20. A(1,13626) -> Halt(13672) via ijjjjjjjjbcbbbccf | |||
21. A(1,43122) -> Halt(43165) via ijjjjjjjjjcccbbf | |||
22. A(1,43124) -> Halt(43165) via ijjjjjjjjjbccbbf | |||
23. A(1,905235) -> Halt(905284) via jjjjjjjjjjjjccjjbbjbf | |||
24. A(1,905237) -> Halt(905284) via jjjjjjjjjjjjbcjjbbjbf | |||
25. A(1,956563) -> Halt(956596) via jjjjjjjjjjjjcd | |||
26. A(1,956565) -> Halt(956596) via jjjjjjjjjjjjbd | |||
27. A(1,1712679) -> Halt(1712746) via jjjjjjjjjjjjjcbcbbcjccjcf | |||
28. A(1,1712681) -> Halt(1712746) via jjjjjjjjjjjjjbbcbbcjccjcf | |||
29. A(1,49818027) -> Halt(49818118) via jjjjjjjjjjjjjjjjccbbjbcccccjcbcd | |||
30. A(1,49818029) -> Halt(49818118) via jjjjjjjjjjjjjjjjbcbbjbcccccjcbcd | |||
31. A(1,77484059) -> Halt(77484100) via jjjjjjjjjjjjjjjjcd | |||
32. A(1,77484061) -> Halt(77484100) via jjjjjjjjjjjjjjjjbd | |||
33. A(1,106744976) -> Halt(106745041) via ijjjjjjjjjjjjjjjjccccjjjbf | |||
34. A(1,106744978) -> Halt(106745041) via ijjjjjjjjjjjjjjjjbcccjjjbf | |||
35. A(1,659939159) -> Halt(659939224) via jjjjjjjjjjjjjjjjjjccjjcbjbd | |||
36. A(1,659939161) -> Halt(659939224) via jjjjjjjjjjjjjjjjjjbcjjcbjbd | |||
37. A(1,3822354579) -> Halt(3822354640) via jjjjjjjjjjjjjjjjjjjjccbbcf | |||
38. A(1,3822354581) -> Halt(3822354640) via jjjjjjjjjjjjjjjjjjjjbcbbcf | |||
39. A(1,6276211875) -> Halt(6276211924) via jjjjjjjjjjjjjjjjjjjjcd | |||
40. A(1,6276211877) -> Halt(6276211924) via jjjjjjjjjjjjjjjjjjjjbd | |||
41. A(1,16380092275) -> Halt(16380092362) via jjjjjjjjjjjjjjjjjjjjjccjcbjjjjbbbbcd | |||
42. A(1,16380092277) -> Halt(16380092362) via jjjjjjjjjjjjjjjjjjjjjbcjcbjjjjbbbbcd | |||
43. A(1,404671372119) -> Halt(404671372210) via jjjjjjjjjjjjjjjjjjjjjjjjcbjcccccccf | |||
44. A(1,404671372121) -> Halt(404671372210) via jjjjjjjjjjjjjjjjjjjjjjjjbbjcccccccf | |||
45. A(1,508373165611) -> Halt(508373165668) via jjjjjjjjjjjjjjjjjjjjjjjjcd | |||
46. A(1,508373165613) -> Halt(508373165668) via jjjjjjjjjjjjjjjjjjjjjjjjbd | |||
47. A(1,3957690125931) -> Halt(3957690126046) via jjjjjjjjjjjjjjjjjjjjjjjjjjcbjcbjjccjjcbbbbcjcd | |||
48. A(1,3957690125933) -> Halt(3957690126046) via jjjjjjjjjjjjjjjjjjjjjjjjjjbbjcbjjccjjcbbbbcjcd | |||
49. A(1,4444131579443) -> Halt(4444131579553) via jjjjjjjjjjjjjjjjjjjjjjjjjjcbjjjbbbcbbbbccbccf | |||
50. A(1,4444131579445) -> Halt(4444131579553) via jjjjjjjjjjjjjjjjjjjjjjjjjjbbjjjbbbcbbbbccbccf | |||
51. A(1,8359489573703) -> Halt(8359489573780) via jjjjjjjjjjjjjjjjjjjjjjjjjjjcccbbd | |||
52. A(1,8359489573705) -> Halt(8359489573780) via jjjjjjjjjjjjjjjjjjjjjjjjjjjbccbbd | |||
53. A(1,26358811020231) -> Halt(26358811020352) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjcbcbjcbcbbccbbcbcjbf | |||
54. A(1,26358811020233) -> Halt(26358811020352) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjbbcbjcbcbbccbbcbcjbf | |||
55. A(1,41178226418867) -> Halt(41178226418932) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjcd | |||
56. A(1,41178226418869) -> Halt(41178226418932) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjbd | |||
57. A(1,81795441578679) -> Halt(81795441578764) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjcbccjcd | |||
58. A(1,81795441578681) -> Halt(81795441578764) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjbbccjcd | |||
59. A(1,1326438094216110) -> Halt(1326438094216285) via ijjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjccbcbbjccjcbjcbjccbbcccccccccf | |||
60. A(1,1326438094216112) -> Halt(1326438094216285) via ijjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjbcbcbbjccjcbjcbjccbbcccccccccf | |||
61. A(1,2031355966425479) -> Halt(2031355966425562) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjcbbcbf | |||
62. A(1,2031355966425481) -> Halt(2031355966425562) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjbbbcbf | |||
63. A(1,3335436339933243) -> Halt(3335436339933316) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjcd | |||
64. A(1,3335436339933245) -> Halt(3335436339933316) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjbd | |||
</pre></div></div> | |||
To determine which halting ''c'' values should get reached by the forward iteration, we can employ a form of backward reasoning. By the nature of this machine, Δ''c'' depends on both the initial (j) run length and the chain length following the run. For longer chains, the length is effectively pseudorandom, so any two sequences of A(1, ''c'') values should eventually hit each other, after which they will have the same values. | |||
If we can find a sufficiently long stretch of consecutive A(1, ''c'') configs that all reach the same halting value, we know that any sequence that reaches that stretch will halt. Conversely, if we find a sufficiently long stretch of A(1, ''c'') configs that skip past a halting value, we know that any sequence that reaches that stretch will skip past the halting value. In the first case, we say that the halting value ''explodes'' in terms of how many A(1, ''c'') configs can reach it; in the second case, we say that the halting value ''dies out''. | |||
The first and currently only known halting value that does not die out is ''H'' = (3<sup>307</sup>−8282708212)/13959275. It it reachable from a very long stretch of consecutive A(1, ''c'') configs up to ''c'' ≤ ''H''−3403055. Thus, assuming the forward iteration reaches this very long stretch, it will halt at A(1, ''H''), unless it has already reached some earlier halting value. | |||
However, we cannot prove that the forward iteration reaches this long stretch instead of skipping past it. Statistically, the expectation is that Δ''c'' = log<sub>3</sub> ''c'' + O(1), but we cannot place any easy bound on how long the chain can become: in principle, there could be an undiscovered A(1, ''c'') config that goes on for 10<sup>1000</sup> steps or more. So if we want to fully prove that this machine halts at or before A(1, ''H''), we must place an upper bound on Δ''c'' for every step leading up to it. But given the size of ''H'', there is no known practical method to compute such an upper bound. | |||
== Equivalence to 1RB0LB0RC_2LC2LA1RA_1RA1LC--- == | == Equivalence to 1RB0LB0RC_2LC2LA1RA_1RA1LC--- == | ||
Revision as of 13:31, 24 October 2025
1RB2LC1RC_2LC---2RB_2LA0LB0RA (bbch) is a BB(3,3) holdout which appears to probviously halt. If it can be proven to halt, it will be the BB(3,3) champion in terms of both steps and tape symbols. However, it could also turn out to be a probviously halting Cryptid.
This is holdout #758 on Justin's 3x3 mugshots. After about 1.8 million steps and up to some relabelling, it is equivalent to holdout #153: 1RB0LB0RC_2LC2LA1RA_1RA1LC--- (bbch). And if you start in state C it is a permutation of the same machine. Together, they simulate a complex set of Collatz-like rules with two decreasing parameters.
After active exploration on the #bb3x3 channel by LegionMammal and dyuan, LegionMammal found (and dyuan confirmed) a configuration A(1,c) (defined here) which halts and for which a huge "wall" of previous A(1, c') values all reach it. This gives strong evidence that the TM probviosly halts since jumping over this wall is very "unlikely".
NOTE: As of 16 Jul 2024 there is a lot more active work on the #bb3x3 channel with LegionMammal and dyuan not reflected here.
dyuan01's Rules
https://discord.com/channels/960643023006490684/1084047886494470185/1224457633176486041
A_1(a, b, c) = 0^inf 1 2^a <C (22)^b (20)^c 0^inf A_2(a, b, c) = 0^inf 1 2^a <A2 (22)^b (20)^c 0^inf B(a, b) = 0^inf 1 2^a <B0 (20)^b 0^inf
| From | To |
|---|---|
| A1(0, b, 2n) | A2(1, b+2n+1, 0) |
| A1(0, b, 2n+1) | A1(1, 0, b+2n+3) |
| A1(m+1, b, 0) | A1(m, 0, b+2) |
| A1(m+1, b, n+1) | A2(m, b+1, n) |
| A2(0, b, 2n) | A1(2b+3, 0, 2n+1) |
| A2(0, b, 2n+1) | A2(2b+3, 2n+1, 0) |
| A2(m+1, b, 0) | B(m, b+2) |
| A2(m+1, b, n+1) | A1(m, b+2, n) |
| B(0, b) | Halt |
| B(m+1, 2n) | A2(m, 2n+1, 0) |
| B(m+1, 2n+1) | A1(m, 0, 2n+3) |
Starting from A1(0, 0, 1) (at step 2).
savask's Rules
https://discord.com/channels/960643023006490684/1084047886494470185/1254085725138190336
Let (m, b, n) = A2(m, b, n) = 0^inf 1 2^m <A2 (22)^b (20)^n 0^inf
(0, b, n) -> (2b+2, 1, n) if n is even
-> (2b, 1, n+3) if n is odd
(1, b, 0) -> Halt
(2, b, 0) -> (0, b+3, 0) if b is even
-> (0, 1, b+5) if b is odd
(m, b, 0) -> (m-2, b+3, 0) if b is even
-> (m-3, 1, b+3) if b is odd
(1, b, n) -> (0, 1, n+b+2) if n is even
-> Halt if n is odd
(2, b, 1) -> Halt if b is even
-> (0, 1, b+5) if b is odd
(m, b, 1) -> (m-3, 1, b+3)
(m, b, n) -> (m-2, b+3, n-2)
https://discord.com/channels/960643023006490684/1084047886494470185/1254306301786198116
step (A2 0 b n) | even n = A2 (2*b+2) 1 n
| otherwise = A2 (2*b) 1 (n+3)
-- From now on m > 0
step (A2 1 b 0) = error $ "Halt A2 1 " ++ show b ++ " 0"
step (A2 2 b 0) | even b = A2 0 (b+3) 0
| otherwise = A2 0 1 (b+5)
step (A2 m b 0) | even b = A2 (m-2) (b+3) 0
| otherwise = A2 (m-3) 1 (b+3)
-- From now on n > 0
step (A2 1 b n) | even n = A2 0 1 (n+b+2)
| otherwise = error $ "Halt A2 1 " ++ show b ++ " " ++ show n
step (A2 2 b 1) | even b = error $ "Halt A2 2 " ++ show b ++ " 1"
| otherwise = A2 0 1 (b+5)
step (A2 m b 1) = A2 (m-3) 1 (b+3)
-- Here m > 1, n > 1
step (A2 m b n) = let d2 = (min m n) `div` 2 in A2 (m - 2*d2) (b + 3*d2) (n - 2*d2) -- Accelerated
Shawn's Rules
https://discord.com/channels/960643023006490684/1084047886494470185/1254307091863048264
We can reduce the set of rules from savask's list a bit by noticing that we can evaluate so that all rules end with c even:
(0, b, 2c) -> (2b+2, 1, 2c) (1, b, 0) -> Halt (1, 2b, 2c) -> (0, 1, 2(b+c+1)) (1, 2b+1, 2c) -> (2, 1, 2(b+c+3)) (a, 2b, 0) -> (a-2, 2b+3, 0) (2, 2b+1, 0) -> (0, 1, 2b+6) (a, 2b+1, 0) -> (a-3, 1, 2b+4) (a, b, c) -> (a-2, b+3, c-2)
Phases
We can think of this going through two different phases. "Even Phase" (where a is even) and "Odd Phase" (where a is odd).
Even Phase: a,c even:
(0, b, 2c) -> (2b+2, 1, 2c)
(2a+2, 2b, 0) -> (2a, 2b+3, 0)
(2, 2b+1, 0) -> (0, 1, 2(b+3))
To Odd Phase:
(2a+4, 2b+1, 0) -> (2a+1, 1, 2b+4)
Odd Phase: a odd, c even
To Halt:
(1, b, 0) -> Halt
(3, 2b, 0) -> (1, 2b+3, 0) -> Halt
To Even Phase:
(1, 2b, 2c+2) -> (0, 1, 2(b+c+2))
(1, 2b+1, 2c+2) -> (0, 1, 2b+2c+5) -> (2, 1, 2(b+c+4))
(2a+5, 2b, 0) -> (2a+3, 2b+3, 0) -> (2a, 1, 2b+6)
(2a+3, 2b+1, 0) -> (2a, 1, 2b+4)
So the only way for this to halt is if it is in "Even Phase" and hits (2k+8, 2k+1, 0) or (4k+12, 4k+3, 0) (which will lead to (1, b, 0) or (3, 2b, 0) eventually).
If a is bigger or smaller, then "Odd Phase" will end going back to "Even Phase" again.
Repeated (0, b, 2c)
Let , then Let
Then if :
Repeated (0, 1, 2c)
https://discord.com/channels/960643023006490684/1084047886494470185/1254635277020954705
Let = 0^inf 1 <A2 22 (20)^2n 0^inf
Notably, when 8 divides (n+1) then this rule can potentially be applied repeatedly.
Ex: if n = 7, then we get:
And we see this starting with which repeats this rule until we get to .
And as n gets way bigger, these ranges of repeat will increase exponentially.
A(a, c) Rules and Timings
Let A(a, c) = A1(a, 0, c) = 0^∞ 1 2^a <C (20)^c 0^∞, where A1(a, b, c) comes from dyuan01's rules. Then the TM satisfies the following rules once it reaches A(0, 1) after 2 steps. Note that rules (a) and (g) aren't actually reachable from the initial condition.
| A(a, c) → | Conditions | Step count | |
|---|---|---|---|
| (a) | A(a−c−1, 3c/2+2) | c ≤ a−1, c ≡ 0 (mod 2) | 3c2+8c+5 |
| (b) | A(a−c−2, 3(c−1)/2+5) | c ≤ a−2, c ≡ 1 (mod 4) | (6c2+31c+37)/2 |
| (c) | A(a−c−4, 3(c−1)/2+8) | c ≤ a−4, c ≡ 3 (mod 4) | 3c2+29c+65 |
| (d) | Halt(3(c−1)/2+7) | c = a−3, c ≡ 3 (mod 4) | (6c2+43c+75)/2 |
| (e) | A(3c+8, 1) | c = a−2, c ≡ 3 (mod 4) | (6c2+37c+63)/2 |
| (f) | Halt(3(c−1)/2+4) | c = a−1, c ≡ 1 (mod 2) | 3c2+8c+6 |
| (g) | Halt(a/2+c+4) | c ≥ a, a ≡ 0, c ≡ 0 (mod 2) | 3a2+5a+9c+24 |
| (h) | A(1, a/2+c+2) | c ≥ a, a ≡ 0, c ≡ 1 (mod 2) | 3a2+3a+5c+11 |
| (i) | A(3a, c−a+4) | c ≥ a, a ≡ 1, c ≡ 0 (mod 2) | 3a2−9a+14c+30 |
| (j) | A(3a+2, c−a+1) | c ≥ a, a ≡ 1, c ≡ 1 (mod 2) | 3a2+5c+6 |
Large-scale behavior
Consider the behavior of this machine starting at A(0, 1). If we start a new line every time rule (h) is applied, we find that it follows chains of steps, each starting from a config of form A(1, c):
A(0,1)
-h> A(1,3) -j> A(5,3) -e> A(17,1) -b> A(14,5)
-b> A(7,11) -j> A(23,5) -b> A(16,11) -c> A(1,23)
-j> A(5,23) -j> A(17,19) -j> A(53,3) -c> A(46,11)
-c> A(31,23) -c> A(4,41)
-h> A(1,45) -j> A(5,45) -j> A(17,41) -j> A(53,25)
-b> A(26,41)
-h> A(1,56) -i> A(3,59) -j> A(11,57) -j> A(35,47)
-j> A(107,13) -b> A(92,23) -c> A(65,41) -b> A(22,65)
-h> A(1,78) -i> A(3,81) -j> A(11,79) -j> A(35,69)
-j> A(107,35) -c> A(68,59) -c> A(5,95) -j> A(17,91)
-j> A(53,75) -j> A(161,23) -c> A(134,41) -b> A(91,65)
-b> A(24,101)
-h> A(1,115) -j> A(5,115) -j> A(17,111) -j> A(53,95)
-j> A(161,43) -c> A(114,71) -c> A(39,113) -j> A(119,75)
-c> A(40,119)
-h> A(1,141) -j> A(5,141) -j> A(17,137) -j> A(53,121)
-j> A(161,69) -b> A(90,107)
-h> A(1,154) -i> ...
If we look at the sequence of applied rule labels, we can see the overall structure of these chains:
A(0,1) h A(1,3) jebbjbcjjjccch A(1,45) jjjbh A(1,56) ijjjbcbh A(1,78) ijjjccjjjcbbh A(1,115) jjjjccjch A(1,141) jjjjbh A(1,154) ijjjjbccbbbjch A(1,194) ijjjjbcbh A(1,218) ijjjjbcjccbcjbcbbjjjcbjcbch A(1,298) ijjjjbh A(1,315) jjjjjccch A(1,341) jjjjjbcjcbbbjch A(1,381) jjjjjbcjbh A(1,405) jjjjjbcjjbh A(1,431) jjjjjch A(1,448) ijjjjch A(1,467) jjjjjch A(1,484) ijjjjjbcbbbcch A(1,524) ijjjjjbcccch A(1,561) jjjjjbh A(1,576) ijjjjjbbbcjjcbjjbcjbbjch A(1,640) ijjjjjbbbh A(1,664) ijjjjjbbch A(1,690) ijjjjjccjbccbjccch
Following a possible (i) and an initial run of (j), the chain alternates between runs of (b)/(c) and runs of (j). Each run of (b)/(c) is of even length, except for the final run which is of odd length. Starting from A(1, c), the length of the initial run of (j) approaches (log3 c − 1). Rules (d), (f), and (h) can only occur after an odd-length run of (b)/(c), while rule (e) can only occur after an even-length run.
Notice how in the sequence of A(1, c) configs, the next c value is always greater than the previous c value, but not extraordinarily greater. In fact, the difference Δc over the course of a chain is roughly proportional to the length of the chain. We can see this if we reparameterize the rules in terms of t = a+2c and d = (c−1)/2, with the invariant that 0 ≤ d ≤ (t−2)/4 at all times:
| T(t, d) → | Conditions | |
|---|---|---|
| (b) | T(t+5, 3d/2+2) | 6d ≤ t−5, d ≡ 0 (mod 2) |
| (c) | T(t+9, 3(d−1)/2+5) | 6d ≤ t−7, d ≡ 1 (mod 2) |
| (d) | Halt(3d+7) | 6d = t−6, d ≡ 1 (mod 2) |
| (e) | T(t+8, 0) | 6d = t−5, d ≡ 1 (mod 2) |
| (f) | Halt(3d+4) | 6d = t−4 |
| (h) | T(t+5, (t−2)/4+1) | 6d ≥ t−2, t ≡ 2 (mod 4) |
| (hi) | T(t+13, t/4+2) | 6d ≥ t−2, t ≡ 0 (mod 4) |
| (j) | T(t+4, 3d−(t−1)/2+1) | 6d ≥ t−3, t ≡ 1 (mod 2) |
In this form, each step increases t by a small positive value, so this explains why Δc between A(1, c) configs depends on the number of steps in the chain.
What determines the number of steps in the chain? As the plot shows, the chain lengths follow a sort of fractal pattern depending on the magnitude of c. To derive this pattern, we first start with our T(t, d) parameterization, combine steps so that t is always odd, and let u = (t−1)/2, so that 0 ≤ d ≤ (u−1)/2. Looking at rules (b), (c), and (j), we find:
| U(u, d) → | Conditions | |
|---|---|---|
| (bb) | U(u+5, (9d+20)/4) | 0 ≤ d ≤ (2u−12)/9, d ≡ 0 (mod 4) |
| (cc) | U(u+9, (9d+35)/4) | 0 ≤ d ≤ (2u−19)/9, d ≡ 1 (mod 4) |
| (bc) | U(u+7, (9d+26)/4) | 0 ≤ d ≤ (2u−12)/9, d ≡ 2 (mod 4) |
| (cb) | U(u+7, (9d+29)/4) | 0 ≤ d ≤ (2u−17)/9, d ≡ 3 (mod 4) |
| (j) | U(u+2, 3d−u+1) | (u−1)/3 ≤ d ≤ (u−1)/2 |
Broadly, it maps d → 9d/4 when 0 < d < 2u/9; hits rule (h) and resets when 2u/9 < d < u/3; and maps d → 3d−u when u/3 < d < u/2. These three subcases form an iterated function system describing a fractal pattern analogous to the ternary Cantor set. The machine checks which interval the ratio 2d/u lies in: if it lies in the middle interval, rule (h) applies, but if it lies in the left or right interval, rules (b), (c), (j) expand its position within that interval, then recursively repeat the check. Similarly to the Cantor set, the fractal has Lebesgue measure 0, so almost all initial points should eventually hit rule (h). As a corollary, the number of steps after the initial (j) run should follow a geometric distribution, so the expected chain length should approach log3 c plus a constant.
The machine halts if the chain ends at rules (d) or (f), which reside at the right edge of the left intervals within the fractal. Certain configs A(1, c) hit one of these rules before hitting rule (h), and these values of c are called halting values. The first few halting values are:
A(1,12) -> Halt(40) via ijjccjcd A(1,14) -> Halt(40) via ijjbcjcd A(1,71) -> Halt(100) via jjjebbccbf A(1,73) -> Halt(100) via jjjjbbccbf A(1,131) -> Halt(148) via jjjjcd A(1,133) -> Halt(148) via jjjjbd A(1,2331) -> Halt(2377) via jjjjjjjcbccccjbf A(1,2333) -> Halt(2377) via jjjjjjjbbccccjbf A(1,2583) -> Halt(2620) via jjjjjjjccbcjbf A(1,2585) -> Halt(2620) via jjjjjjjbcbcjbf
As a rule, halting values always come in pairs with a difference of 2, except in the unlikely case that a chain hits rule (e) before halting. They are common for small values of c, but soon become exponentially rare. In fact, there only exist 64 total halting values up to c = 3.4×1015, and the first 58 are known not to be reached by the forward iteration.
1. A(1,12) -> Halt(40) via ijjccjcd 2. A(1,14) -> Halt(40) via ijjbcjcd 3. A(1,71) -> Halt(100) via jjjebbccbf 4. A(1,73) -> Halt(100) via jjjjbbccbf 5. A(1,131) -> Halt(148) via jjjjcd 6. A(1,133) -> Halt(148) via jjjjbd 7. A(1,2331) -> Halt(2377) via jjjjjjjcbccccjbf 8. A(1,2333) -> Halt(2377) via jjjjjjjbbccccjbf 9. A(1,2583) -> Halt(2620) via jjjjjjjccbcjbf 10. A(1,2585) -> Halt(2620) via jjjjjjjbcbcjbf 11. A(1,3195) -> Halt(3241) via jjjjjjjcbjbbccjcf 12. A(1,3197) -> Halt(3241) via jjjjjjjbbjbbccjcf 13. A(1,6306) -> Halt(6358) via ijjjjjjjcbjcccbcd 14. A(1,6308) -> Halt(6358) via ijjjjjjjbbjcccbcd 15. A(1,7167) -> Halt(7204) via jjjjjjjjcbcbbd 16. A(1,7169) -> Halt(7204) via jjjjjjjjbbcbbd 17. A(1,11787) -> Halt(11812) via jjjjjjjjcd 18. A(1,11789) -> Halt(11812) via jjjjjjjjbd 19. A(1,13624) -> Halt(13672) via ijjjjjjjjccbbbccf 20. A(1,13626) -> Halt(13672) via ijjjjjjjjbcbbbccf 21. A(1,43122) -> Halt(43165) via ijjjjjjjjjcccbbf 22. A(1,43124) -> Halt(43165) via ijjjjjjjjjbccbbf 23. A(1,905235) -> Halt(905284) via jjjjjjjjjjjjccjjbbjbf 24. A(1,905237) -> Halt(905284) via jjjjjjjjjjjjbcjjbbjbf 25. A(1,956563) -> Halt(956596) via jjjjjjjjjjjjcd 26. A(1,956565) -> Halt(956596) via jjjjjjjjjjjjbd 27. A(1,1712679) -> Halt(1712746) via jjjjjjjjjjjjjcbcbbcjccjcf 28. A(1,1712681) -> Halt(1712746) via jjjjjjjjjjjjjbbcbbcjccjcf 29. A(1,49818027) -> Halt(49818118) via jjjjjjjjjjjjjjjjccbbjbcccccjcbcd 30. A(1,49818029) -> Halt(49818118) via jjjjjjjjjjjjjjjjbcbbjbcccccjcbcd 31. A(1,77484059) -> Halt(77484100) via jjjjjjjjjjjjjjjjcd 32. A(1,77484061) -> Halt(77484100) via jjjjjjjjjjjjjjjjbd 33. A(1,106744976) -> Halt(106745041) via ijjjjjjjjjjjjjjjjccccjjjbf 34. A(1,106744978) -> Halt(106745041) via ijjjjjjjjjjjjjjjjbcccjjjbf 35. A(1,659939159) -> Halt(659939224) via jjjjjjjjjjjjjjjjjjccjjcbjbd 36. A(1,659939161) -> Halt(659939224) via jjjjjjjjjjjjjjjjjjbcjjcbjbd 37. A(1,3822354579) -> Halt(3822354640) via jjjjjjjjjjjjjjjjjjjjccbbcf 38. A(1,3822354581) -> Halt(3822354640) via jjjjjjjjjjjjjjjjjjjjbcbbcf 39. A(1,6276211875) -> Halt(6276211924) via jjjjjjjjjjjjjjjjjjjjcd 40. A(1,6276211877) -> Halt(6276211924) via jjjjjjjjjjjjjjjjjjjjbd 41. A(1,16380092275) -> Halt(16380092362) via jjjjjjjjjjjjjjjjjjjjjccjcbjjjjbbbbcd 42. A(1,16380092277) -> Halt(16380092362) via jjjjjjjjjjjjjjjjjjjjjbcjcbjjjjbbbbcd 43. A(1,404671372119) -> Halt(404671372210) via jjjjjjjjjjjjjjjjjjjjjjjjcbjcccccccf 44. A(1,404671372121) -> Halt(404671372210) via jjjjjjjjjjjjjjjjjjjjjjjjbbjcccccccf 45. A(1,508373165611) -> Halt(508373165668) via jjjjjjjjjjjjjjjjjjjjjjjjcd 46. A(1,508373165613) -> Halt(508373165668) via jjjjjjjjjjjjjjjjjjjjjjjjbd 47. A(1,3957690125931) -> Halt(3957690126046) via jjjjjjjjjjjjjjjjjjjjjjjjjjcbjcbjjccjjcbbbbcjcd 48. A(1,3957690125933) -> Halt(3957690126046) via jjjjjjjjjjjjjjjjjjjjjjjjjjbbjcbjjccjjcbbbbcjcd 49. A(1,4444131579443) -> Halt(4444131579553) via jjjjjjjjjjjjjjjjjjjjjjjjjjcbjjjbbbcbbbbccbccf 50. A(1,4444131579445) -> Halt(4444131579553) via jjjjjjjjjjjjjjjjjjjjjjjjjjbbjjjbbbcbbbbccbccf 51. A(1,8359489573703) -> Halt(8359489573780) via jjjjjjjjjjjjjjjjjjjjjjjjjjjcccbbd 52. A(1,8359489573705) -> Halt(8359489573780) via jjjjjjjjjjjjjjjjjjjjjjjjjjjbccbbd 53. A(1,26358811020231) -> Halt(26358811020352) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjcbcbjcbcbbccbbcbcjbf 54. A(1,26358811020233) -> Halt(26358811020352) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjbbcbjcbcbbccbbcbcjbf 55. A(1,41178226418867) -> Halt(41178226418932) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjcd 56. A(1,41178226418869) -> Halt(41178226418932) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjbd 57. A(1,81795441578679) -> Halt(81795441578764) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjcbccjcd 58. A(1,81795441578681) -> Halt(81795441578764) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjbbccjcd 59. A(1,1326438094216110) -> Halt(1326438094216285) via ijjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjccbcbbjccjcbjcbjccbbcccccccccf 60. A(1,1326438094216112) -> Halt(1326438094216285) via ijjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjbcbcbbjccjcbjcbjccbbcccccccccf 61. A(1,2031355966425479) -> Halt(2031355966425562) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjcbbcbf 62. A(1,2031355966425481) -> Halt(2031355966425562) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjbbbcbf 63. A(1,3335436339933243) -> Halt(3335436339933316) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjcd 64. A(1,3335436339933245) -> Halt(3335436339933316) via jjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjbd
To determine which halting c values should get reached by the forward iteration, we can employ a form of backward reasoning. By the nature of this machine, Δc depends on both the initial (j) run length and the chain length following the run. For longer chains, the length is effectively pseudorandom, so any two sequences of A(1, c) values should eventually hit each other, after which they will have the same values.
If we can find a sufficiently long stretch of consecutive A(1, c) configs that all reach the same halting value, we know that any sequence that reaches that stretch will halt. Conversely, if we find a sufficiently long stretch of A(1, c) configs that skip past a halting value, we know that any sequence that reaches that stretch will skip past the halting value. In the first case, we say that the halting value explodes in terms of how many A(1, c) configs can reach it; in the second case, we say that the halting value dies out.
The first and currently only known halting value that does not die out is H = (3307−8282708212)/13959275. It it reachable from a very long stretch of consecutive A(1, c) configs up to c ≤ H−3403055. Thus, assuming the forward iteration reaches this very long stretch, it will halt at A(1, H), unless it has already reached some earlier halting value.
However, we cannot prove that the forward iteration reaches this long stretch instead of skipping past it. Statistically, the expectation is that Δc = log3 c + O(1), but we cannot place any easy bound on how long the chain can become: in principle, there could be an undiscovered A(1, c) config that goes on for 101000 steps or more. So if we want to fully prove that this machine halts at or before A(1, H), we must place an upper bound on Δc for every step leading up to it. But given the size of H, there is no known practical method to compute such an upper bound.
Equivalence to 1RB0LB0RC_2LC2LA1RA_1RA1LC---
1RB0LB0RC_2LC2LA1RA_1RA1LC--- (bbch), #153, eventually becomes equivalent to this machine. As found by @Legion, after running the #153 machine for 1,790,901 steps, if one permutes the states A,C, and B and exchanges 1 for 2 and L for R, it has the same configuration as TM #758 after it has run 1,841,608 steps.
History
LegionMammal's rough timeline of this TM on 30 Apr 2025 (Discord link):
- The machine (and its sibling) pass straight through various rounds of cleverly-written deciders
- dyuan posts his set of rules and looks into it a bit, Justin notes that he'd briefly looked at it some time back
- Shawn and savask write up some acceleration schemes, find empirical evidence that it repeatedly comes close to halting, and speculate that it may actually halt after some period of time
- I take a crack at it myself, this time in terms of chains starting from
A(1,c)configs, find somecvalues leading to a halt (showing that there's no obvious structural barrier), and conjecture some heuristics for how long it should take to reach such a haltingcvalue - dyuan and I nail down the ideas of 'halter families' (collections of infinitely many halting
cvalues so we don't have to brute-force them) and 'reachability analysis' (obtaining a strong probvious guess of whether acvalue will or won't occur in the machine's actual forward behavior, assuming it hasn't halted beforehand) - dyuan and I race to find a halting
cvalue that 'explodes' (passes the reachability analysis), first within the 'trivial' halter family to no avail, then within all halter families (writing a program to enumerate halter families is extremely fiddly, at this point I treat some of my own code as a black box not to be touched) - By dint of a somewhat more performant program, I find (and dyuan confirms) the we all know and love, probviously sealing the machine's fate