Fractran: Difference between revisions
→Vector Representation: Note how size works in vec rep |
→Deciders: link FAST |
||
| (74 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
'''Fractran''' (originally styled FRACTRAN) is an esoteric Turing complete model of computation invented by John Conway in 1987.<ref>Conway, John H. (1987). "FRACTRAN: A Simple Universal Programming Language for Arithmetic". ''Open Problems in Communication and Computation''. Springer-Verlag New York, Inc. pp. 4–26. <nowiki>http://doi.org/10.1007/978-1-4612-4808-8_2</nowiki></ref> In this model a program is simply a finite list of fractions, the program state is an integer. For more details see https://en.wikipedia.org/wiki/FRACTRAN | '''Fractran''' (originally styled FRACTRAN) is an esoteric [[Turing complete]] model of computation invented by John Conway in 1987.<ref>Conway, John H. (1987). "FRACTRAN: A Simple Universal Programming Language for Arithmetic". ''Open Problems in Communication and Computation''. Springer-Verlag New York, Inc. pp. 4–26. <nowiki>http://doi.org/10.1007/978-1-4612-4808-8_2</nowiki></ref> In this model a program is simply a finite list of fractions (rational numbers), the program state is an integer. For more details see https://en.wikipedia.org/wiki/FRACTRAN. | ||
'''BB_fractran'''(n) or '''BBf'''(n) is the Busy Beaver function for Fractran programs. | Discord user Coda came up with a way to transform any Fractran program into a Turing Machine, see [https://discord.com/channels/960643023006490684/1438019511155691521/1441844795613122560 source]. | ||
'''BB_fractran'''(n) or '''BBf'''(n) is the Busy Beaver function for Fractran programs. Holdouts lists by Daniel Yuan: [https://github.com/int-y1/BBFractran/blob/main/holdout/README.md Holdouts lists] | |||
== Definition == | == Definition == | ||
A fractran program is a list of rational numbers <math>[q_0, q_1, ... q_{k-1}]</math>called rules and a fractran state is an integer <math>s \in \mathbb{Z}</math>. We say that a rule <math>q_i</math> applies to state <math>s</math> if <math>s \cdot q_i \in \mathbb{Z}</math>. If no rule applies, we say that the computation has halted otherwise we apply the first applicable rule at each step. In that case we say <math>s \to t</math> and <math>t = s \cdot q_i</math> and <math>i = \min \{ i : s \cdot q_i \in \mathbb{Z} \}</math>. We say that a program has runtime N (or halts in N steps) starting in state s if <math>s \ | A fractran program is a list of rational numbers <math>[q_0, q_1, ... q_{k-1}]</math>called rules and a fractran state is an integer <math>s \in \mathbb{Z}</math>. The numerator and denominator of any rational number fraction do not share any prime factors (they are in reduced form). We say that a rule <math>q_i</math> applies to state <math>s</math> if <math>s \cdot q_i \in \mathbb{Z}</math>. If no rule applies, we say that the computation has halted otherwise we apply the first applicable rule at each step. In that case we say <math>s \to t</math> and <math>t = s \cdot q_i</math> and <math>i = \min \{ i : s \cdot q_i \in \mathbb{Z} \}</math>. As with [[Turing machines]], we will write <math>s \xrightarrow{N} t</math> if <math>s \to s_1 \to \cdots \to s_{N-1} \to t </math> (s goes to t after N steps) and <math>s \to^* t</math> or <math>s \to^+ t</math> if <math>s \xrightarrow{N} t</math> for some N≥0 or N≥1 (respectively). We say that a program has runtime N (or halts in N steps) starting in state s if <math>s \xrightarrow{N} t</math> and computation halts on t. | ||
Let <math>\Omega(n)</math> be the total number of prime factors of a positive integer n. In other words <math>\Omega( | Let <math>\Omega(n)</math> be the total number of prime factors of a positive integer n. In other words, <math>\Omega(2^{a_0} 3^{a_1} \cdots p_n^{a_n}) = \sum_{k=0}^n a_n</math>. Then given a rule <math>\frac{a}{b} </math> we say that <math>\text{size} \left( \frac{a}{b} \right) = \Omega(a) + \Omega(b) </math>. And the size of a fractran program <math>[q_0, q_1, ... q_{k-1}]</math> is <math>k + \sum_{i=0}^{k-1} \text{size}(q_i) </math>. | ||
BB_fractran(n) or BBf(n) is the maximum runtime starting in state 2 for all halting fractran programs of size n. It is a non-computable function akin to the [[Busy Beaver Functions]] since Fractran is Turing Complete. | BB_fractran(n) or BBf(n) is the maximum runtime starting in state 2 for all halting fractran programs of size n. It is a non-computable function akin to the [[Busy Beaver Functions]] since Fractran is Turing Complete. | ||
| Line 27: | Line 29: | ||
In this representation, it becomes much easier to reason about fractran programs and describe general rules. It is also very easy to calculate the size of a rule or program in vector representation. It is the sum of absolute values of all elements in the matrix + number of rules (number of rows). | In this representation, it becomes much easier to reason about fractran programs and describe general rules. It is also very easy to calculate the size of a rule or program in vector representation. It is the sum of absolute values of all elements in the matrix + number of rules (number of rows). | ||
=== Relationship to VAS / Petri Nets === | |||
Using vector representation, fractran programs are a deterministic version of [[wikipedia:Vector_addition_system|Vector Addition Systems (VAS)]] (and, equivalently, [[wikipedia:Petri_net|Petri Nets]]). VAS are identical to fractran programs in vector representation except that the rules are unordered and non-deterministic, they are used to model distributed systems where precise order of rule execution cannot be predicted. Interestingly, many problems about VAS are actually decidable, but their runtimes are extremely slow. Notably, the reachability problem (given states A and B are there a sequence of rules so that <math>A \to^* B</math>) is "Ackermann-complete" meaning that the optimal algorithm has worst-case runtime akin to the famously fast-growing Ackermann function.<ref>Czerwiński, Wojciech; Orlikowski, Łukasz (2021). ''Reachability in Vector Addition Systems is Ackermann-complete''. 2021 IEEE 62nd Annual Symposium on Foundations of Computer Science (FOCS). https://arxiv.org/abs/2104.13866.</ref> | |||
== Deciders == | |||
[[File:Fractran deciders.png|alt=Fractran deciders|thumb|All Fractran deciders summarized and their relations, shared by Daniel Yuan on [https://discord.com/channels/960643023006490684/1438019511155691521/1439001835904958655 14 Nov 2025]]]Many specialized deciders have been invented to prove fractran programs non-halting. See image at right. There is [https://discord.com/channels/960643023006490684/1438019511155691521/1449775657554022531 an extra decider, <code>spanning vectors masked,</code>] which is very effective, but is not present on the picture. Also, some holdouts were removed by [[User:Sligocki|Shawn Ligocki]] with [https://lsv.ens-paris-saclay.fr/Software/fast/ FAST] (Fast Acceleration of Symbolic Transition systems), a pre-existing general tool. | |||
== Champions == | == Champions == | ||
The table of champions is split into two pieces: the first for small champions (up to BBf(14)) which all share the same relatively simple behavior (sequential programs) is collapsed by default; the second for champions BBf(15) and beyond which have more complex and varied behavior. | |||
All small champions as well as the first few larger ones were discovered and proven maximal by Jason Yuen (@-d) in their initial enumeration on [https://discord.com/channels/960643023006490684/1362008236118511758/1434033599094587595 1 Nov 2025]. | |||
<div class="toccolours mw-collapsible mw-collapsed">'''Small Champions'''<div class="mw-collapsible-content"> | |||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
| Line 35: | Line 48: | ||
!Example Champion | !Example Champion | ||
!Vector Representation | !Vector Representation | ||
|- | |- | ||
| 2 || 1 || <code>[1/2]</code> | | 2 || 1 || <code>[1/2]</code> | ||
| Line 117: | Line 127: | ||
0 & 0 & -1 | 0 & 0 & -1 | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
|} | |||
</div></div> | |||
{| class="wikitable" | |||
|+ | |||
!n | |||
!BBf(n) | |||
!Example Champion | |||
!Vector Representation | |||
!Champion Found | |||
!Holdouts Proven | |||
|- | |- | ||
| 15 || 28 || <code>[1/45, 4/5, 3/2, 25/3]</code> | | 15 || 28 || <code>[1/45, 4/5, 3/2, 25/3]</code> | ||
| Line 125: | Line 146: | ||
0 & -1 & 2 | 0 & -1 & 2 | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
|Jason Yuen (@-d) [https://discord.com/channels/960643023006490684/1362008236118511758/1434033599094587595 1 Nov 2025] | |||
|Jason Yuen (@-d) [https://discord.com/channels/960643023006490684/1362008236118511758/1434033599094587595 1 Nov 2025] | |||
|- | |- | ||
| 16 || 53 || <code>[1/45, 4/5, 3/2, 125/3]</code> | | 16 || 53 || <code>[1/45, 4/5, 3/2, 125/3]</code> | ||
| Line 133: | Line 156: | ||
0 & -1 & 3 | 0 & -1 & 3 | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
|Jason Yuen (@-d) [https://discord.com/channels/960643023006490684/1362008236118511758/1434033599094587595 1 Nov 2025] | |||
|Jason Yuen (@-d) [https://discord.com/channels/960643023006490684/1362008236118511758/1434033599094587595 1 Nov 2025] | |||
|- | |- | ||
| 17 || 107 || <code>[5/6, 49/2, 3/5, 40/7]</code> | | 17 || 107 || <code>[5/6, 49/2, 3/5, 40/7]</code> | ||
| Line 141: | Line 166: | ||
3 & 0 & 1 & -1 | 3 & 0 & 1 & -1 | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
|Jason Yuen (@-d) [https://discord.com/channels/960643023006490684/1362008236118511758/1434313398799175710 1 Nov 2025] | |||
|Daniel Yuan (@dyuan01) [https://discord.com/channels/960643023006490684/1362008236118511758/1434771877376557086 3 Nov 2025] | |||
|- | |- | ||
| 18 || 211 || <code>[5/6, 49/2, 3/5, 80/7]</code> | | 18 || 211 || <code>[5/6, 49/2, 3/5, 80/7]</code> | ||
| Line 149: | Line 176: | ||
4 & 0 & 1 & -1 | 4 & 0 & 1 & -1 | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
|Jason Yuen (@-d) [https://discord.com/channels/960643023006490684/1362008236118511758/1435313806493614131 4 Nov 2025] | |||
|Jason Yuen (@-d) [https://discord.com/channels/960643023006490684/1362008236118511758/1436661215911870584 8 Nov 2025] | |||
|- | |- | ||
| 19 || | | 19 || 370 || <code>[5/6, 49/2, 3/5, 160/7]</code> | ||
|<math>\begin{bmatrix} | |<math>\begin{bmatrix} | ||
-1 & -1 & 1 & 0 \\ | -1 & -1 & 1 & 0 \\ | ||
| Line 157: | Line 186: | ||
5 & 0 & 1 & -1 | 5 & 0 & 1 & -1 | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
|@creeperman7002 [https://discord.com/channels/960643023006490684/1362008236118511758/1435763150489387090 5 Nov 2025] | |||
|Decider: Daniel Yuan (@dyuan01) [https://discord.com/channels/960643023006490684/1438019511155691521/1438558242388312165 13 Nov 2025] | |||
3 Holdouts: Racheline & Shawn Ligocki | |||
|- | |||
|20 | |||
|≥ 746 | |||
|<code>[7/15, 22/3, 6/77, 5/2, 9/5]</code> | |||
|<math>\begin{bmatrix} | |||
0 & -1 & -1 & 1 & 0 \\ | |||
1 & -1 & 0 & 0 & 1 \\ | |||
1 & 1 & 0 & -1 & -1 \\ | |||
-1 & 0 & 1 & 0 & 0 \\ | |||
0 & 2 & -1 & 0 & 0 | |||
\end{bmatrix}</math> | |||
|Jason Yuen (@-d) [https://discord.com/channels/960643023006490684/1438019511155691521/1438480761169776733 13 Nov 2025] | |||
|8 holdouts<sup>[https://github.com/int-y1/BBFractran/blob/main/holdout/]</sup> remain. [https://discord.com/channels/960643023006490684/1438019511155691521/1449827092823806023 14 Dec 2025] | |||
|- | |||
|21 | |||
|≥ 31,957,632 | |||
|<code>[7/15, 4/3, 27/14, 5/2, 9/5]</code> | |||
|<math>\begin{bmatrix} | |||
0 & -1 & -1 & 1 \\ | |||
2 & -1 & 0 & 0 \\ | |||
-1 & 3 & 0 & -1 \\ | |||
-1 & 0 & 1 & 0 \\ | |||
0 & 2 & -1 & 0 | |||
\end{bmatrix}</math> | |||
|Jason Yuen (@-d) [https://discord.com/channels/960643023006490684/1438019511155691521/1439759182587891894 16 Nov 2025] | |||
|349 holdouts<sup>[https://github.com/int-y1/BBFractran/blob/main/holdout]</sup> remain. [https://discord.com/channels/960643023006490684/1438019511155691521/1449829243914813516 14 Dec 2025] | |||
|- | |||
|22 | |||
|<math>> 1.146 \times 10^{62}</math> | |||
|<code>[1/12, 9/10, 14/3, 11/2, 5/7, 3/11]</code> | |||
|<math>\begin{bmatrix} | |||
-2 & -1 & 0 & 0 & 0 \\ | |||
-1 & 2 & -1 & 0 & 0 \\ | |||
1 & -1 & 0 & 1 & 0 \\ | |||
-1 & 0 & 0 & 0 & 1 \\ | |||
0 & 0 & 1 & -1 & 0 \\ | |||
0 & 1 & 0 & 0 & -1 | |||
\end{bmatrix}</math> | |||
|Shawn Ligocki (@sligocki) [https://discord.com/channels/960643023006490684/1438019511155691521/1448912286713384961 11 Dec 2025] and Jason Yuen (@-d)<sup>[https://discord.com/channels/960643023006490684/1438019511155691521/1448953682237460480 <nowiki>[3]</nowiki>]</sup> | |||
|7085 holdouts<sup>[https://github.com/int-y1/BBFractran/blob/main/holdout/ <nowiki>[4]</nowiki>]</sup> remain. [https://discord.com/channels/960643023006490684/1438019511155691521/1449837530974388377 14 Dec 2025] | |||
|- | |||
|23 | |||
| | |||
| | |||
| | |||
| | |||
|Known [[Cryptid|Cryptids]]: | |||
# Frankenstein's Monster | |||
# Antihydra-like Cryptid | |||
|} | |} | ||
=== Behavior of Champions === | |||
==== Sequential programs ==== | |||
All champions up to BBf(14) have very simple behavior. They are all of the form: <math>\left[ \frac{3^{a_1}}{2}, \frac{5^{a_2}}{3}, ... \frac{p_n^{a_k}}{p_{k-1}}, \frac{1}{p_k} \right]</math> or in vector representation (limited to k=4): | |||
<math display="block">\begin{bmatrix} | |||
-1 & a_1 & 0 & 0 & 0 \\ | |||
0 & -1 & a_2 & 0 & 0 \\ | |||
0 & 0 & -1 & a_3 & 0 \\ | |||
0 & 0 & 0 & -1 & a_4 \\ | |||
0 & 0 & 0 & 0 & -1 | |||
\end{bmatrix}</math> | |||
These champions repeatedly apply the rules in sequence, never going back to a previous rule. They apply the first rule until they've exhausted all 2s, then the second rule until they've exhausted all 3s, etc. They have a runtime of <math>1 + a_1 + a_1 a_2 + a_1 a_2 a_3 + \cdots = \sum_{i=0}^k \prod_{j=1}^i a_j</math> and size <math>2k+2 + \sum_{i=1}^k a_i</math>. This grows linearly for k=1 (BBf(5) to BBf(10)) and quadratically for k=2 (BBf(11) to BBf(14)). Letting k grow with the size, the maximum runtime grows exponentially in the program size. | |||
==== BBf(15) Family ==== | |||
The BBf(15) and BBf(16) champions are members of a family of programs (parameterized by <math>n \ge 1</math>): | |||
<math display="block">\begin{bmatrix} | |||
0 & -2 & -1 \\ | |||
2 & 0 & -1 \\ | |||
-1 & 1 & 0 \\ | |||
0 & -1 & n | |||
\end{bmatrix}</math> | |||
Let a = 2, b = 3, and c = 5. | |||
The BBf(15) champion (n = 2) implements this iteration: | |||
<math display="block">\begin{array}{lcl} | |||
b^0 & \xrightarrow{0} & \text{halt} \\ | |||
b^1 & \xrightarrow{7} & b^4 \\ | |||
b^2 & \xrightarrow{7} & b^5 \\ | |||
b^3 & \xrightarrow{5} & b^2 \\ | |||
b^4 & \xrightarrow{5} & b^3 \\ | |||
b^{n+5} & \xrightarrow{3} & b^n \\ | |||
\end{array}</math> | |||
which follows a permutation-like trajectory: <math>a \xrightarrow{1} b^1 \to b^4 \to b^3 \to b^2 \to b^5 \to b^0 \to \text{halt}</math> | |||
The BBf(16) champion (n = 3) implements this iteration: | |||
<math display="block">\begin{array}{lcl} | |||
b^0 & \xrightarrow{0} & \text{halt} \\ | |||
b^1 & \xrightarrow{10} & b^6 \\ | |||
b^2 & \xrightarrow{10} & b^7 \\ | |||
b^3 & \xrightarrow{8} & b^4 \\ | |||
b^4 & \xrightarrow{8} & b^5 \\ | |||
b^5 & \xrightarrow{6} & b^2 \\ | |||
b^6 & \xrightarrow{6} & b^3 \\ | |||
b^{n+7} & \xrightarrow{4} & b^n \\ | |||
\end{array}</math> | |||
which follows a permutation-like trajectory: <math>a \xrightarrow{1} b^1 \to b^6 \to b^3 \to b^4 \to b^5 \to b^2 \to b^7 \to b^0 \to \text{halt}</math> | |||
==== BBf(17) Family ==== | |||
The BBf(17) to BBf(19) champions are members of a family of programs (parameterized by <math>m,n \ge 0</math>) | |||
<math display="block">\begin{bmatrix} | |||
-1 & -1 & 1 & 0 \\ | |||
-1 & 0 & 0 & n \\ | |||
0 & 1 & -1 & 0 \\ | |||
m & 0 & 1 & -1 | |||
\end{bmatrix}</math> | |||
which have size <math>m+n+12</math> | |||
This family obeys the following rules: | |||
# <math>[1, 0, 0, 0] \xrightarrow{1} [0, 0, 0, n]</math> | |||
# if d≥1 and b≤m:<math display="block">[0, b, 0, d] \xrightarrow{m+b+2} [0, b+1, 0, d - 1 + n(m-b)]</math> | |||
# if d≥1 and b≥m:<math display="block">[0, b, 0, d] \xrightarrow{2m+2} [0, b+1, 0, d - 1]</math> | |||
#if d=0: [0,b,0,d] has halted | |||
and furthermore these rules are applied in order since b is always increasing (and d is eventually decreasing). Combining these together we get runtime:<math display="block">1 + n(m+1)(m(m+1)+2) - \frac{m(m+1)}{2}</math> | |||
The optimal choices for n,m for various program sizes are: | |||
{| class="wikitable" | |||
|+ | |||
!Size | |||
!n | |||
!m | |||
!Runtime | |||
|- | |||
|16 | |||
|1 | |||
|3 | |||
|51 | |||
|- | |||
|17 | |||
|2 | |||
|3 | |||
|107 | |||
|- | |||
|18 | |||
|2 | |||
|4 | |||
|211 | |||
|- | |||
|19 | |||
|2 | |||
|5 | |||
|370 | |||
|- | |||
|20 | |||
|2 | |||
|6 | |||
|596 | |||
|- | |||
|21 | |||
|3 | |||
|6 | |||
|904 | |||
|} | |||
==== BBf(20) ==== | |||
The BBf(20) champion (running 746 steps): | |||
<math display="block">\begin{bmatrix} | |||
0 & -1 & -1 & 1 & 0 \\ | |||
1 & -1 & 0 & 0 & 1 \\ | |||
1 & 1 & 0 & -1 & -1 \\ | |||
-1 & 0 & 1 & 0 & 0 \\ | |||
0 & 2 & -1 & 0 & 0 | |||
\end{bmatrix}</math> | |||
This program implements a [[Collatz-like]] iteration. Let <math>C(n) = [0, 0, n, 2, 0]</math>, then: | |||
<math display="block">\begin{array}{lcl} | |||
[1,0,0,0,0] & \xrightarrow{49} & C(2) \\ | |||
C(3k) & \xrightarrow{3k} & \text{halt} \\ | |||
C(3k+1) & \xrightarrow{11k+22} & C(4k+3) \\ | |||
C(3k+2) & \xrightarrow{11k+22} & C(4k+4) \\ | |||
\end{array}</math> | |||
which follows the reasonably "lucky" trajectory: | |||
<math display="block">C(2) \to C(4) \to C(7) \to C(11) \to C(16) \to C(23) \to C(32) \to C(44) \to C(60) \to \text{halt}</math> | |||
==== BBf(21) ==== | |||
The BBf(21) champion (running >31M steps): | |||
<math display="block">\begin{bmatrix} | |||
0 & -1 & -1 & 1 \\ | |||
2 & -1 & 0 & 0 \\ | |||
-1 & 3 & 0 & -1 \\ | |||
-1 & 0 & 1 & 0 \\ | |||
0 & 2 & -1 & 0 | |||
\end{bmatrix}</math> | |||
This program implements a Collatz-like iteration. Let <math>D(n) = [0, 0, n, 0]</math>, then:<sup>[https://discord.com/channels/960643023006490684/1438019511155691521/1439779341365022852]</sup> | |||
<math display="block">\begin{array}{lcl} | |||
[1,0,0,0,0] & \xrightarrow{1} & D(1) \\ | |||
D(3k) & \xrightarrow{k} & \text{halt} \\ | |||
D(3k+1) & \xrightarrow{21k+7} & C(10k+4) \\ | |||
D(3k+2) & \xrightarrow{21k+14} & C(10k+7) \\ | |||
\end{array}</math> | |||
which follows the reasonably "lucky" trajectory: | |||
<math display="block">\begin{array}{ll} | |||
D(1) & \to D(4) \to D(14) \to D(47) \to D(157) \to D(524) \to D(1747) \to D(5824) \to D(19414) \\ | |||
& \to D(64714) \to D(215714) \to D(719047) \to D(2396824) \to D(7989414) \to \text{halt} \\ | |||
\end{array}</math> | |||
==== BBf(22) ==== | |||
The BBf(22) champion (running <math>> 10^{62}</math> steps): | |||
<math display="block">\begin{bmatrix} | |||
-2 & -1 & 0 & 0 & 0 \\ | |||
-1 & 2 & -1 & 0 & 0 \\ | |||
1 & -1 & 0 & 1 & 0 \\ | |||
-1 & 0 & 0 & 0 & 1 \\ | |||
0 & 0 & 1 & -1 & 0 \\ | |||
0 & 1 & 0 & 0 & -1 | |||
\end{bmatrix}</math> | |||
This program implements a [[Collatz-like]] unbiased psuedo-random walk. Let <math>S(x,y) = [0, 0, x, 0, y]</math>, then:<sup>[https://discord.com/channels/960643023006490684/1438019511155691521/1449118888142049421]</sup> | |||
<math display="block">\begin{array}{lcl} | |||
[1,0,0,0,0] & \xrightarrow{1} & S(0,1) \\ | |||
S(x, 0) & = & \text{halt} \\ | |||
S(3k, y+1) & \xrightarrow{14k+4} & S(5k+1, y+1) \\ | |||
S(3k+1, y+1) & \xrightarrow{14k+10} & S(5k+3, y+2) \\ | |||
S(3k+2, y+1) & \xrightarrow{14k+12} & S(5k+4, y) \\ | |||
\end{array}</math> | |||
This random walk iterates 275 times until it halts reaching a maximum y value of 14 at iteration 111: | |||
<math display="block">\begin{array}{ll} | |||
S(0,1) & \to S(1,1) \to S(3,2) \to S(6,2) \to S(11, 2) \to S(19, 1) \to S(33, 2) \to S(56, 2) \to S(94, 1) \\ | |||
& \to S(158, 2) \to S(264, 1) \to S(441, 1) \to S(736, 1) \to S(1228, 2) \to S(2048, 3) \\ | |||
& \vdots \\ | |||
& \to S(4065328691604230522442358, 13) \\ | |||
& \to S(6775547819340384204070598, 14) \\ | |||
& \to S(11292579698900640340117664, 13) \\ | |||
& \vdots \\ | |||
& \to S(27930059557111373800280446055462487109112535227834136644, 2) \\ | |||
& \to S(46550099261852289667134076759104145181854225379723561074, 1) \\ | |||
& \to S(77583498769753816111890127931840241969757042299539268458, 2) \\ | |||
& \to S(129305831282923026853150213219733736616261737165898780764, 1) \\ | |||
& \to S(215509718804871711421917022032889561027102895276497967941, 1) \\ | |||
& \to S(359182864674786185703195036721482601711838158794163279903, 2) \\ | |||
& \vdots \\ | |||
& \to S(5894430516013404355095519889620117404469367857588232386361874, 2) \\ | |||
& \to S(9824050860022340591825866482700195674115613095980387310603124, 1) \\ | |||
& \to S(16373418100037234319709777471166992790192688493300645517671874, 0) | |||
\end{array}</math> | |||
== Cryptids == | |||
=== Frankenstein's Monster === | |||
"Frankenstein's Monster" is a size 23 [[Cryptid]]. It was created by tweaking a single instruction in the size 22 champion. This tweak switches it from a unbiased random walk to a biased one and thus makes halting probviously impossible. It is called Frankenstein's Monster since it was found by a combination of exhaustive search and hand design.<sup>[https://discord.com/channels/960643023006490684/1438019511155691521/1449138938215141478]</sup> | |||
<code>[1/12, 9/10, 14/3, 121/2, 5/7, 3/11]</code> <math display="block">\begin{bmatrix} | |||
-2 & -1 & 0 & 0 & 0 \\ | |||
-1 & 2 & -1 & 0 & 0 \\ | |||
1 & -1 & 0 & 1 & 0 \\ | |||
-1 & 0 & 0 & 0 & 2 \\ | |||
0 & 0 & 1 & -1 & 0 \\ | |||
0 & 1 & 0 & 0 & -1 | |||
\end{bmatrix}</math> | |||
It's behavior is extremely similar to the size 22 champion. Let <math>S(x,y) = [0, 0, x, 0, y]</math>, then: | |||
<math display="block">\begin{array}{lcl} | |||
[1,0,0,0,0] & \xrightarrow{1} & S(0,2) \\ | |||
S(x, 0) & = & \text{halt} \\ | |||
S(3k, y+1) & \xrightarrow{14k+4} & S(5k+1, y+2) \\ | |||
S(3k+1, y+1) & \xrightarrow{14k+10} & S(5k+3, y+4) \\ | |||
S(3k+2, y+1) & \xrightarrow{14k+12} & S(5k+4, y) \\ | |||
\end{array}</math> | |||
with the only difference that the y values now change by {+1,+3,-1} depending on the value of x mod 3 (instead of {0,+1,-1} in the original size 22 program). The x values follow the exact same path as in the original size 22 champion, but the y values quickly grow linearly with the number of iterations (as expected by the random model): | |||
0: S(0, 1) @ 1 (0.00s) | |||
100_000: S(10^22_185, 100171) @ 10^22_186 (0.87s) | |||
200_000: S(10^44_370, 200187) @ 10^44_371 (3.42s) | |||
300_000: S(10^66_555, 300759) @ 10^66_556 (7.68s) | |||
400_000: S(10^88_740, 400451) @ 10^88_741 (13.64s) | |||
500_000: S(10^110_925, 500421) @ 10^110_925 (21.28s) | |||
600_000: S(10^133_109, 600351) @ 10^133_110 (30.62s) | |||
700_000: S(10^155_294, 700319) @ 10^155_295 (41.64s) | |||
800_000: S(10^177_479, 799911) @ 10^177_480 (54.30s) | |||
900_000: S(10^199_664, 900259) @ 10^199_665 (68.59s) | |||
1_000_000: S(10^221_849, 1000853) @ 10^221_850 (84.51s) | |||
... | |||
4_000_000: S(10^887_395, 4000201) @ 10^887_396 (1474.02s) | |||
... | |||
27_500_000: S(10^6_100_841, 27512703) @ 10^6_100_842 (87616.45s) | |||
=== Antihydra-like Cryptid === | |||
This Cryptid is a size 23 [[Cryptid]]. This Cryptid was [https://discord.com/channels/960643023006490684/1438019511155691521/1449293536737361973 constructed by Maksandchael] by tweaking Frankenstein's Monster to make it as similar to [[Antihydra]] as possible. <code>[9/10, 1/6, 1331/2, 14/3, 5/7, 3/11]</code> | |||
<math display="block">\begin{bmatrix} | |||
-1 & 2 & -1 & 0 & 0 \\ | |||
-1 & -1 & 0 & 0 & 0 \\ | |||
-1 & 0 & 0 & 0 & 3 \\ | |||
1 & -1 & 0 & 1 & 0 \\ | |||
0 & 0 & 1 & -1 & 0 \\ | |||
0 & 1 & 0 & 0 & -1 | |||
\end{bmatrix}</math><syntaxhighlight> | |||
H(a, b) = [0, 0, a-2, 0, b] | |||
Start -> H(2, 3) | |||
H(2a, b) -> H(3a, b+2) | |||
H(2a+1, b+1) -> H(3a+1, b) | |||
H(a,0) -> halt | |||
</syntaxhighlight> | |||
=== Hydra === | |||
A size 25 program was produced and golfed by hand to simulate [[Hydra]] rules ([https://discord.com/channels/960643023006490684/1438019511155691521/1449829146040467681 Discord]): | |||
<code>[363/14, 125/2, 22/21, 1/3, 7/11, 14/5]</code> | |||
<math display="block"> | |||
\begin{bmatrix} | |||
-1 & 1 & 0 & -1 & 2 \\ | |||
-1 & 0 & 3 & 0 & 0 \\ | |||
1 & -1 & 0 & -1 & 1 \\ | |||
0 & -1 & 0 & 0 & 0 \\ | |||
0 & 0 & 0 & 1 & -1 \\ | |||
1 & 0 & -1 & 1 & 0 | |||
\end{bmatrix} | |||
</math> | |||
The intended interpretation is that if we let <math>S(h,w) = [1, 0, w, h-3, 0] | |||
</math> then it follows the following rules: | |||
<math display="block">\begin{array}{lcl} | |||
[1,0,\dots] & = & S(3, 0) \\ | |||
S(2k, 0) & \to^* & \text{halt} \\ | |||
S(2k, w+1) & \to^* & S(3k, w) \\ | |||
S(2k+1, w) & \to^* & S(3k+1, w+2) \\ | |||
\end{array}</math> | |||
=== BMO1 === | |||
A size 36 program was produced by hand to simulate [[BMO1]] rules ([https://discord.com/channels/960643023006490684/1438019511155691521/1440018895212642424 Discord]): | |||
<code>[153/55, 2/11, 26/35, 3/7, 11/17, 7/13, 25/6, 55/2, 14/3]</code> | |||
<math display="block"> | |||
\begin{bmatrix} | |||
0 & 2 & -1 & 0 & -1 & 0 & 1 \\ | |||
1 & 0 & 0 & 0 & -1 & 0 & 0 \\ | |||
1 & 0 & -1 & -1 & 0 & 1 & 0 \\ | |||
0 & 1 & 0 & -1 & 0 & 0 & 0 \\ | |||
0 & 0 & 0 & 0 & 1 & 0 & -1 \\ | |||
0 & 0 & 0 & 1 & 0 & -1 & 0 \\ | |||
-1 & -1 & 2 & 0 & 0 & 0 & 0 \\ | |||
-1 & 0 & 1 & 0 & 1 & 0 & 0 \\ | |||
1 & -1 & 0 & 1 & 0 & 0 & 0 | |||
\end{bmatrix} | |||
</math> | |||
Let <math>A(a,b) = [a, b, 0, 0, 0, 0, 0]</math>, then it follows the rules: | |||
<math display="block">\begin{array}{lcl} | |||
[1,0,\dots] & \to^* & A(1, 2) \\ | |||
A(a, b) & \to^* & A(a-b, 4b+2) & \text{if } a > b \\ | |||
A(a, b) & \to^* & A(2a+1, b-a) & \text{if } a < b \\ | |||
A(a, b) & \to^* & \text{Halt} & \text{if } a = b \\ | |||
\end{array}</math> | |||
=== BMO 6 (“Space Needle”) === | |||
A size 48 program was produced by hand to simulate [https://wiki.bbchallenge.org/wiki/1RB1LA_1LC0RE_1LF1LD_0RB0LA_1RC1RE_---0LD BMO 6] rules ([https://discord.com/channels/960643023006490684/1438019511155691521/1441137371046482071 Discord]) | |||
<code>[77/2, 2/99, 17/33, 13/11, 285/119, 17/19, 1375/51, 1/17, 3/5, 243/7, 10/13]</code> | |||
<math>\begin{bmatrix} | |||
-1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 \\ | |||
1 & -2 & 0 & 0 & -1 & 0 & 0 & 0 \\ | |||
0 & -1 & 0 & 0 & -1 & 0 & 1 & 0 \\ | |||
0 & 0 & 0 & 0 & -1 & 1 & 0 & 0 \\ | |||
0 & 1 & 1 & -1 & 0 & 0 & -1 & 1 \\ | |||
0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 \\ | |||
0 & -1 & 3 & 0 & 1 & 0 & -1 & 0 \\ | |||
0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 \\ | |||
0 & 1 & -1 & 0 & 0 & 0 & 0 & 0 \\ | |||
0 & 5 & 0 & -1 & 0 & 0 & 0 & 0 \\ | |||
1 & 0 & 1 & 0 & 0 & -1 & 0 & 0 | |||
\end{bmatrix}</math><syntaxhighlight>A(a, b) = B^a C^b E or B^(a-2) C^b D E | |||
Start: A(7, 1) | |||
A(1, b) --> halt | |||
A(2a, b) --> A(5a+b+2, 1) | |||
A(2a+1, b) --> A(b-1, b+c+3)</syntaxhighlight> | |||
== References == | == References == | ||
<references /> | <references /> | ||
[[Category:Functions]] | |||
Latest revision as of 21:16, 23 December 2025
Fractran (originally styled FRACTRAN) is an esoteric Turing complete model of computation invented by John Conway in 1987.[1] In this model a program is simply a finite list of fractions (rational numbers), the program state is an integer. For more details see https://en.wikipedia.org/wiki/FRACTRAN.
Discord user Coda came up with a way to transform any Fractran program into a Turing Machine, see source.
BB_fractran(n) or BBf(n) is the Busy Beaver function for Fractran programs. Holdouts lists by Daniel Yuan: Holdouts lists
Definition
A fractran program is a list of rational numbers called rules and a fractran state is an integer . The numerator and denominator of any rational number fraction do not share any prime factors (they are in reduced form). We say that a rule applies to state if . If no rule applies, we say that the computation has halted otherwise we apply the first applicable rule at each step. In that case we say and and . As with Turing machines, we will write if (s goes to t after N steps) and or if for some N≥0 or N≥1 (respectively). We say that a program has runtime N (or halts in N steps) starting in state s if and computation halts on t.
Let be the total number of prime factors of a positive integer n. In other words, . Then given a rule we say that . And the size of a fractran program is .
BB_fractran(n) or BBf(n) is the maximum runtime starting in state 2 for all halting fractran programs of size n. It is a non-computable function akin to the Busy Beaver Functions since Fractran is Turing Complete.
Vector Representation
Fractran programs are not easy to interpret, in fact it may be completely unclear at first that they can perform any computation at all. One of the key insights is to represent all numbers (states and rules) in their prime factorization form. For example, we can use a vector to represent the number .
Let the vector representation (for a sufficiently large n) for a state be and the vector representation for a rule be (Note that this is just an extension of the original definition extended to allow negative ).
Now, rule q applies to state s iff (all components of the vector are ≥0) and if then . So the fractran multiplication model is completely equivalent to the vector adding model. For presentation, we will represent a fractran program with a matrix where each row is the vector representation for a rule.
For example, the BBf(15) champion ([1/45, 4/5, 3/2, 25/3]) in vector representation would be:
In this representation, it becomes much easier to reason about fractran programs and describe general rules. It is also very easy to calculate the size of a rule or program in vector representation. It is the sum of absolute values of all elements in the matrix + number of rules (number of rows).
Relationship to VAS / Petri Nets
Using vector representation, fractran programs are a deterministic version of Vector Addition Systems (VAS) (and, equivalently, Petri Nets). VAS are identical to fractran programs in vector representation except that the rules are unordered and non-deterministic, they are used to model distributed systems where precise order of rule execution cannot be predicted. Interestingly, many problems about VAS are actually decidable, but their runtimes are extremely slow. Notably, the reachability problem (given states A and B are there a sequence of rules so that ) is "Ackermann-complete" meaning that the optimal algorithm has worst-case runtime akin to the famously fast-growing Ackermann function.[2]
Deciders
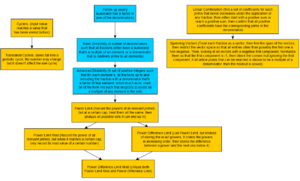
Many specialized deciders have been invented to prove fractran programs non-halting. See image at right. There is an extra decider, spanning vectors masked, which is very effective, but is not present on the picture. Also, some holdouts were removed by Shawn Ligocki with FAST (Fast Acceleration of Symbolic Transition systems), a pre-existing general tool.
Champions
The table of champions is split into two pieces: the first for small champions (up to BBf(14)) which all share the same relatively simple behavior (sequential programs) is collapsed by default; the second for champions BBf(15) and beyond which have more complex and varied behavior.
All small champions as well as the first few larger ones were discovered and proven maximal by Jason Yuen (@-d) in their initial enumeration on 1 Nov 2025.
| n | BBf(n) | Example Champion | Vector Representation |
|---|---|---|---|
| 2 | 1 | [1/2]
|
|
| 3 | 1 | [3/2]
|
|
| 4 | 1 | [9/2]
|
|
| 5 | 2 | [3/2, 1/3]
|
|
| 6 | 3 | [9/2, 1/3]
|
|
| 7 | 4 | [27/2, 1/3]
|
|
| 8 | 5 | [81/2, 1/3]
|
|
| 9 | 6 | [243/2, 1/3]
|
|
| 10 | 7 | [729/2, 1/3]
|
|
| 11 | 10 | [27/2, 25/3, 1/5]
|
|
| 12 | 13 | [81/2, 25/3, 1/5]
|
|
| 13 | 17 | [81/2, 125/3, 1/5]
|
|
| 14 | 21 | [243/2, 125/3, 1/5]
|
| n | BBf(n) | Example Champion | Vector Representation | Champion Found | Holdouts Proven |
|---|---|---|---|---|---|
| 15 | 28 | [1/45, 4/5, 3/2, 25/3]
|
Jason Yuen (@-d) 1 Nov 2025 | Jason Yuen (@-d) 1 Nov 2025 | |
| 16 | 53 | [1/45, 4/5, 3/2, 125/3]
|
Jason Yuen (@-d) 1 Nov 2025 | Jason Yuen (@-d) 1 Nov 2025 | |
| 17 | 107 | [5/6, 49/2, 3/5, 40/7]
|
Jason Yuen (@-d) 1 Nov 2025 | Daniel Yuan (@dyuan01) 3 Nov 2025 | |
| 18 | 211 | [5/6, 49/2, 3/5, 80/7]
|
Jason Yuen (@-d) 4 Nov 2025 | Jason Yuen (@-d) 8 Nov 2025 | |
| 19 | 370 | [5/6, 49/2, 3/5, 160/7]
|
@creeperman7002 5 Nov 2025 | Decider: Daniel Yuan (@dyuan01) 13 Nov 2025
3 Holdouts: Racheline & Shawn Ligocki | |
| 20 | ≥ 746 | [7/15, 22/3, 6/77, 5/2, 9/5]
|
Jason Yuen (@-d) 13 Nov 2025 | 8 holdouts[1] remain. 14 Dec 2025 | |
| 21 | ≥ 31,957,632 | [7/15, 4/3, 27/14, 5/2, 9/5]
|
Jason Yuen (@-d) 16 Nov 2025 | 349 holdouts[2] remain. 14 Dec 2025 | |
| 22 | [1/12, 9/10, 14/3, 11/2, 5/7, 3/11]
|
Shawn Ligocki (@sligocki) 11 Dec 2025 and Jason Yuen (@-d)[3] | 7085 holdouts[4] remain. 14 Dec 2025 | ||
| 23 | Known Cryptids:
|
Behavior of Champions
Sequential programs
All champions up to BBf(14) have very simple behavior. They are all of the form: or in vector representation (limited to k=4):
These champions repeatedly apply the rules in sequence, never going back to a previous rule. They apply the first rule until they've exhausted all 2s, then the second rule until they've exhausted all 3s, etc. They have a runtime of and size . This grows linearly for k=1 (BBf(5) to BBf(10)) and quadratically for k=2 (BBf(11) to BBf(14)). Letting k grow with the size, the maximum runtime grows exponentially in the program size.
BBf(15) Family
The BBf(15) and BBf(16) champions are members of a family of programs (parameterized by ):
Let a = 2, b = 3, and c = 5.
The BBf(15) champion (n = 2) implements this iteration:
which follows a permutation-like trajectory:
The BBf(16) champion (n = 3) implements this iteration:
which follows a permutation-like trajectory:
BBf(17) Family
The BBf(17) to BBf(19) champions are members of a family of programs (parameterized by )
which have size
This family obeys the following rules:
- if d≥1 and b≤m:
- if d≥1 and b≥m:
- if d=0: [0,b,0,d] has halted
and furthermore these rules are applied in order since b is always increasing (and d is eventually decreasing). Combining these together we get runtime:
The optimal choices for n,m for various program sizes are:
| Size | n | m | Runtime |
|---|---|---|---|
| 16 | 1 | 3 | 51 |
| 17 | 2 | 3 | 107 |
| 18 | 2 | 4 | 211 |
| 19 | 2 | 5 | 370 |
| 20 | 2 | 6 | 596 |
| 21 | 3 | 6 | 904 |
BBf(20)
The BBf(20) champion (running 746 steps):
This program implements a Collatz-like iteration. Let , then:
which follows the reasonably "lucky" trajectory:
BBf(21)
The BBf(21) champion (running >31M steps):
This program implements a Collatz-like iteration. Let , then:[3]
which follows the reasonably "lucky" trajectory:
BBf(22)
The BBf(22) champion (running steps):
This program implements a Collatz-like unbiased psuedo-random walk. Let , then:[4]
This random walk iterates 275 times until it halts reaching a maximum y value of 14 at iteration 111:
Cryptids
Frankenstein's Monster
"Frankenstein's Monster" is a size 23 Cryptid. It was created by tweaking a single instruction in the size 22 champion. This tweak switches it from a unbiased random walk to a biased one and thus makes halting probviously impossible. It is called Frankenstein's Monster since it was found by a combination of exhaustive search and hand design.[5]
[1/12, 9/10, 14/3, 121/2, 5/7, 3/11]
It's behavior is extremely similar to the size 22 champion. Let , then:
with the only difference that the y values now change by {+1,+3,-1} depending on the value of x mod 3 (instead of {0,+1,-1} in the original size 22 program). The x values follow the exact same path as in the original size 22 champion, but the y values quickly grow linearly with the number of iterations (as expected by the random model):
0: S(0, 1) @ 1 (0.00s) 100_000: S(10^22_185, 100171) @ 10^22_186 (0.87s) 200_000: S(10^44_370, 200187) @ 10^44_371 (3.42s) 300_000: S(10^66_555, 300759) @ 10^66_556 (7.68s) 400_000: S(10^88_740, 400451) @ 10^88_741 (13.64s) 500_000: S(10^110_925, 500421) @ 10^110_925 (21.28s) 600_000: S(10^133_109, 600351) @ 10^133_110 (30.62s) 700_000: S(10^155_294, 700319) @ 10^155_295 (41.64s) 800_000: S(10^177_479, 799911) @ 10^177_480 (54.30s) 900_000: S(10^199_664, 900259) @ 10^199_665 (68.59s) 1_000_000: S(10^221_849, 1000853) @ 10^221_850 (84.51s) ... 4_000_000: S(10^887_395, 4000201) @ 10^887_396 (1474.02s) ... 27_500_000: S(10^6_100_841, 27512703) @ 10^6_100_842 (87616.45s)
Antihydra-like Cryptid
This Cryptid is a size 23 Cryptid. This Cryptid was constructed by Maksandchael by tweaking Frankenstein's Monster to make it as similar to Antihydra as possible. [9/10, 1/6, 1331/2, 14/3, 5/7, 3/11]
H(a, b) = [0, 0, a-2, 0, b]
Start -> H(2, 3)
H(2a, b) -> H(3a, b+2)
H(2a+1, b+1) -> H(3a+1, b)
H(a,0) -> haltHydra
A size 25 program was produced and golfed by hand to simulate Hydra rules (Discord):
[363/14, 125/2, 22/21, 1/3, 7/11, 14/5]
The intended interpretation is that if we let then it follows the following rules:
BMO1
A size 36 program was produced by hand to simulate BMO1 rules (Discord):
[153/55, 2/11, 26/35, 3/7, 11/17, 7/13, 25/6, 55/2, 14/3]
Let , then it follows the rules:
BMO 6 (“Space Needle”)
A size 48 program was produced by hand to simulate BMO 6 rules (Discord)
[77/2, 2/99, 17/33, 13/11, 285/119, 17/19, 1375/51, 1/17, 3/5, 243/7, 10/13]
A(a, b) = B^a C^b E or B^(a-2) C^b D E
Start: A(7, 1)
A(1, b) --> halt
A(2a, b) --> A(5a+b+2, 1)
A(2a+1, b) --> A(b-1, b+c+3)References
- ↑ Conway, John H. (1987). "FRACTRAN: A Simple Universal Programming Language for Arithmetic". Open Problems in Communication and Computation. Springer-Verlag New York, Inc. pp. 4–26. http://doi.org/10.1007/978-1-4612-4808-8_2
- ↑ Czerwiński, Wojciech; Orlikowski, Łukasz (2021). Reachability in Vector Addition Systems is Ackermann-complete. 2021 IEEE 62nd Annual Symposium on Foundations of Computer Science (FOCS). https://arxiv.org/abs/2104.13866.