Hydra function: Difference between revisions
m Corrected minor errors |
Rewrote Properties Section, added material from the Antihydra page that is better suited here |
||
| Line 1: | Line 1: | ||
[[File:Hydra Spiral.png|thumb|185px|A spiral-like figure that gives the first few terms of the Hydra sequences with initial values 2, 5, 8, 11, 14, and 17.]] | [[File:Hydra Spiral.png|thumb|185px|A spiral-like figure that gives the first few terms of the Hydra sequences with initial values 2, 5, 8, 11, 14, and 17.]] | ||
The '''Hydra function''' is a [[Collatz-like]] function defined as: | The '''Hydra function''' is a [[Collatz-like]] function defined as: | ||
<math display="block">\textstyle H(n)\equiv n+\ | <math display="block">\textstyle H(n)\equiv n+\big\lfloor\frac{1}{2}n\big\rfloor=\Big\lfloor\frac{3}{2}n\Big\rfloor=\begin{cases} | ||
\frac{3n}{2}&\text{if }n\equiv0\pmod{2},\\ | \frac{3n}{2}&\text{if }n\equiv0\pmod{2},\\ | ||
\frac{3n-1}{2}&\text{if }n\equiv1\pmod{2}.\\ | \frac{3n-1}{2}&\text{if }n\equiv1\pmod{2}.\\ | ||
| Line 42: | Line 42: | ||
\end{array}</math> | \end{array}</math> | ||
|} | |} | ||
Already, both machines appear to | Already, both machines appear to be very similar. They have one parameter that increases exponentially with growth factor <math display="inline">\frac{3}{2}</math> and another that takes a pseudo-random walk. Below, the exponentially increasing variables are described by integer sequences: | ||
{|class="wikitable" | {|class="wikitable" | ||
! Hydra !! Antihydra | ! Hydra !! Antihydra | ||
| Line 49: | Line 49: | ||
|<math display="block">a_0=4,a_{n+1}=\begin{cases}\frac{3a_n+4}{2}&\text{if }a_n\equiv0\pmod{2}\\\frac{3a_n+3}{2}&\text{if }a_n\equiv1\pmod{2}\end{cases}</math> | |<math display="block">a_0=4,a_{n+1}=\begin{cases}\frac{3a_n+4}{2}&\text{if }a_n\equiv0\pmod{2}\\\frac{3a_n+3}{2}&\text{if }a_n\equiv1\pmod{2}\end{cases}</math> | ||
|} | |} | ||
This | This will make demonstrating the transformation easier. Now we will define a new integer sequence based on the old one and discover the recursive rules for that sequence. This new sequence is <math display="inline">b_n=\frac{1}{3}a_n+2</math> and <math>b_n=a_n+4</math> for Hydra and Antihydra respectively. We start by using <math>b_{n+1}</math> instead and substituting <math>a_{n+1}</math> for its recursive formula. By doing so, we get: | ||
{|class="wikitable" | {|class="wikitable" | ||
! Hydra !! Antihydra | ! Hydra !! Antihydra | ||
| Line 63: | Line 63: | ||
|<math display="block">b_0=8,b_{n+1}=\begin{cases}\frac{3(b_n-4)+12}{2}&\text{if }b_n-4\equiv0\pmod{2}\\\frac{3(b_n-4)+11}{2}&\text{if }b_n-4\equiv1\pmod{2}\end{cases}</math> | |<math display="block">b_0=8,b_{n+1}=\begin{cases}\frac{3(b_n-4)+12}{2}&\text{if }b_n-4\equiv0\pmod{2}\\\frac{3(b_n-4)+11}{2}&\text{if }b_n-4\equiv1\pmod{2}\end{cases}</math> | ||
|} | |} | ||
The <math>\text{if}</math> statements amount to checking if <math>b_n</math> is even or odd. After simplifying, we are done: | |||
{|class="wikitable" | {|class="wikitable" | ||
! Hydra !! Antihydra | ! Hydra !! Antihydra | ||
| Line 70: | Line 70: | ||
|<math display="block">b_0=8,b_{n+1}=\begin{cases}\frac{3b_n}{2}&\text{if }b_n\equiv0\pmod{2}\\\frac{3b_n-1}{2}&\text{if }b_n\equiv1\pmod{2}\end{cases}</math> | |<math display="block">b_0=8,b_{n+1}=\begin{cases}\frac{3b_n}{2}&\text{if }b_n\equiv0\pmod{2}\\\frac{3b_n-1}{2}&\text{if }b_n\equiv1\pmod{2}\end{cases}</math> | ||
|} | |} | ||
Now that we have demonstrated a strong similarity in the behaviour of both Turing machines, we can return to using the high-level rules. Doing that while | Now that we have demonstrated a strong similarity in the behaviour of both Turing machines, we can return to using the high-level rules. Doing that while considering the step counts yields the final result. | ||
</div></div> | </div></div> | ||
Under these rules, the halting problem for Hydra is about whether repeatedly applying the function <math>H(n)</math>, starting with <math>n=3</math>, will eventually generate more even terms than twice the number of odd terms. Similarly, Antihydra halts if and only if repeatedly applying <math>H(n)</math>, starting with <math>n=8</math>, will eventually generate more odd terms than twice the number of even terms. | |||
== Coding the Hydra function == | |||
The Hydra function's simple definition allows one to write computer programs that simulate Hydra and Antihydra. The following Python program is a straightforward Hydra simulator based on the Hydra function: | |||
<syntaxhighlight lang="python" line="1"> | |||
# 'a' and 'b' fulfill the same purpose as in the Hydra rules. | |||
a = 3 | |||
b = 0 | |||
# As long as Hydra has not halted, 'b' remains greater than -1. | |||
while b != -1: | |||
# If 'a' is even, decrement 'b', otherwise increase 'b' by 2. | |||
if a % 2 == 0: | |||
b -= 1 | |||
else: | |||
b += 2 | |||
# This performs H(a) = a + floor(a/2). | |||
a += a//2 | |||
</syntaxhighlight> | |||
Replacing <code>a = 3</code> with <code>a = 8</code> and swapping <code>b -= 1</code> for <code>b += 2</code> turns this program into an Antihydra simulator. | |||
==Properties== | ==Properties== | ||
The Hydra function can be rewritten as follows: | The Hydra function can be rewritten as follows: | ||
| Line 78: | Line 96: | ||
H(2n+1)&=&3n+1.\\ | H(2n+1)&=&3n+1.\\ | ||
\end{array}</math> | \end{array}</math> | ||
Now | Now assume that for some positive integer <math>s</math> and every odd integer <math>t</math>, <math>H^s(2^st)=3^st</math> and <math>H^s(2^st+1)=3^st+1</math>, where <math>H^i(n)</math> is function iteration. Notice that we can write <math>2^{s+1}t=2\cdot2^st</math> and <math>2^{s+1}t+1=2\cdot2^st+1</math>, so if we apply <math>H</math> to these numbers, we get <math>H(2\cdot2^st)=3\cdot 2^st</math> and <math>H(2\cdot2^st+1)=3\cdot2^st+1</math>. Now, if we apply <math>H</math> to these numbers <math>s</math> times, we get <math>H^{s+1}\big(2^{s+1}t\big)=H^s(2^s\cdot3t)=3^{s+1}t</math> and <math>H^{s+1}\big(2^{s+1}t+1\big)=H^s(2^s\cdot3t+1)=3^{s+1}t+1</math>. Therefore, by mathematical induction we have proved the following formulas: | ||
<math | |||
H( | |||
<math display="block">\begin{array}{l} | <math display="block">\begin{array}{l} | ||
H^s(2^st)&=&3^st,\\ | H^s(2^st)&=&3^st,\\ | ||
| Line 104: | Line 117: | ||
where <math display="inline">f_3(s,t,a)=(2a-3+2s)s+\frac{3t^2(9^s-4^s)}{5}</math> and <math display="inline">f_4(s,t)=\frac{3t^2(9^s-4^s)}{5}-7s</math>. | where <math display="inline">f_3(s,t,a)=(2a-3+2s)s+\frac{3t^2(9^s-4^s)}{5}</math> and <math display="inline">f_4(s,t)=\frac{3t^2(9^s-4^s)}{5}-7s</math>. | ||
|} | |} | ||
== Visualizations == | |||
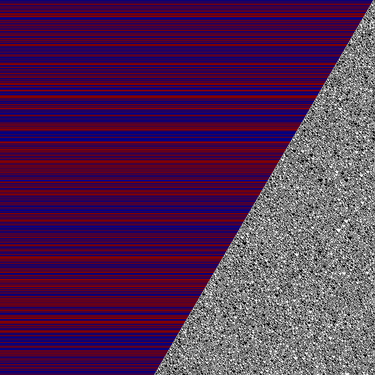
The four images below depict the first 1000 values of four Hydra sequences with different initial values. Each row of pixels shows a number in binary on the right and its parity on the left (blue for even, red for odd): | |||
<gallery mode=packed heights="250"> | |||
File:HydraFunction-StartingValue2.png|Starting value 2. There are 492 even numbers and 508 odd numbers. | |||
File:HydraFunction-StartingValue5.png|Starting value 5. There are 497 even numbers and 503 odd numbers. | |||
File:Antihydra increasing value.png|Starting value 8. There are 499 even numbers and 501 odd numbers. | |||
File:HydraFunction-StartingValue11.png|Starting value 11. There are 481 even numbers and 519 odd numbers. | |||
</gallery> | |||
Revision as of 22:12, 14 April 2025
The Hydra function is a Collatz-like function defined as: It is named as such because of its connection to the unsolved halting problems for the Cryptids Hydra and Antihydra. Due to its simplicity, simulations for both of these Turing machines utilize this function instead of what can initially be proven.
Relationship to Hydra and Antihydra
Using the Hydra function, we can obtain simplified rules for Hydra and Antihydra:
| Hydra | Antihydra |
|---|---|
| Let : | Let : |
Recall the high-level rules for Hydra and Antihydra:
| Hydra | Antihydra |
|---|---|
| Let : | Let : |
Already, both machines appear to be very similar. They have one parameter that increases exponentially with growth factor and another that takes a pseudo-random walk. Below, the exponentially increasing variables are described by integer sequences:
| Hydra | Antihydra |
|---|---|
This will make demonstrating the transformation easier. Now we will define a new integer sequence based on the old one and discover the recursive rules for that sequence. This new sequence is and for Hydra and Antihydra respectively. We start by using instead and substituting for its recursive formula. By doing so, we get:
| Hydra | Antihydra |
|---|---|
After that, we can substitute for its solution in terms of . What results is the following:
| Hydra | Antihydra |
|---|---|
The statements amount to checking if is even or odd. After simplifying, we are done:
| Hydra | Antihydra |
|---|---|
Now that we have demonstrated a strong similarity in the behaviour of both Turing machines, we can return to using the high-level rules. Doing that while considering the step counts yields the final result.
Under these rules, the halting problem for Hydra is about whether repeatedly applying the function , starting with , will eventually generate more even terms than twice the number of odd terms. Similarly, Antihydra halts if and only if repeatedly applying , starting with , will eventually generate more odd terms than twice the number of even terms.
Coding the Hydra function
The Hydra function's simple definition allows one to write computer programs that simulate Hydra and Antihydra. The following Python program is a straightforward Hydra simulator based on the Hydra function:
# 'a' and 'b' fulfill the same purpose as in the Hydra rules.
a = 3
b = 0
# As long as Hydra has not halted, 'b' remains greater than -1.
while b != -1:
# If 'a' is even, decrement 'b', otherwise increase 'b' by 2.
if a % 2 == 0:
b -= 1
else:
b += 2
# This performs H(a) = a + floor(a/2).
a += a//2
Replacing a = 3 with a = 8 and swapping b -= 1 for b += 2 turns this program into an Antihydra simulator.
Properties
The Hydra function can be rewritten as follows: Now assume that for some positive integer and every odd integer , and , where is function iteration. Notice that we can write and , so if we apply to these numbers, we get and . Now, if we apply to these numbers times, we get and . Therefore, by mathematical induction we have proved the following formulas: This optimization can be directly applied to the high-level rules for Hydra and Antihydra, producing this result:
| Hydra | Antihydra |
|---|---|
| Let :
where and . |
Let :
where and . |
Visualizations
The four images below depict the first 1000 values of four Hydra sequences with different initial values. Each row of pixels shows a number in binary on the right and its parity on the left (blue for even, red for odd):
-
Starting value 2. There are 492 even numbers and 508 odd numbers.
-
Starting value 5. There are 497 even numbers and 503 odd numbers.
-
Starting value 8. There are 499 even numbers and 501 odd numbers.
-
Starting value 11. There are 481 even numbers and 519 odd numbers.