Antihydra

Unsolved problem:

Does Antihydra run forever?

1RB1RA_0LC1LE_1LD1LC_1LA0LB_1LF1RE_---0RA (bbch)

Artistic depiction of Antihydra by Jadeix

Antihydra is the first BB(6) Cryptid to be identified. It operates by repeatedly applying the function $H(n)=\lfloor \frac{3}{2}n\rfloor$, starting with $n=8$. Determining whether this Turing machine halts requires solving the Collatz-like mathematical problem of whether there eventually exists a step at which $H(n)$ has been applied to (strictly) more than twice as many odd as even numbers. Proving a result remains challenging due to the lack of an exploitable pattern in the sequence's parities, although probabilistic arguments based on random walks suggest Antihydra has a minuscule chance of halting.

Description

The transition table of Antihydra.

Antihydra basically repeatedly modifies the integer ordered pair $(x,y)$ starting at $(0,4)$, which is represented on the tape as $x$ consecutive $1$s and $y$ consecutive $1$s, separated by a single $0$. It does this by "borrowing" a $0$ from the right side and, through a series of back-and-forth head movements, "moves" this $0$ toward the one separating $x$ and $y$, two units at a time. As this happens, the head visits new cells on the right, which has the effect of there being about $\frac{3}{2}$ times as many $1$s on the tape when the distance has been closed. After that, $x$ and $y$ are updated. If the previous value of $x$ was even, then $y$ becomes $y+2$. Otherwise, $y$ becomes $y-1$ or Antihydra halts if $y$ was 0.

Let $H(n)=\lfloor \frac{3}{2}n\rfloor$, and $a_k$ and $b_k$ be integer sequences defined below: $$\begin{array}{llll}{a}_0=0,& a_{k+1}=\{\begin{array}{ll}{a}_k+2& \text{if }{b}_k\equiv 0(\mathrm{mod}2)\\ a_k-1& \text{if }{b}_k\equiv 1(\mathrm{mod}2)\\ \end{array},& b_0=8,& b_{k+1}=H(b_k).\end{array}$$ Antihydra halts if and only if there exists any number $i$ for which $a_i<0$.

Attributions

Community trophy to be awarded to the first person or group who solves the Antihydra problem

Antihydra and its pseudo-random behaviour were reported on Discord by mxdys on 28 June 2024, and Racheline discovered the high-level rules soon after, where it was found to be closely related to Hydra; in particular, the roles of even and odd numbers are switched. This is why the machine was named Antihydra.

Analysis

Let $A(a,b):=0^{\mathrm{\infty }}{1}^{a}01^b\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}{0}^{\mathrm{\infty }}$. Then, $$\begin{array}{lll}A(a,2b)& \stackrel{2a+3b^2+12b+11}{\to }& A(a+2,3b+2),\\ A(0,2b+1)& \stackrel{3b^2+9b-1}{\to }& 0^{\mathrm{\infty }}\text{<mrow data-mjx-texclass="ORD"><mo><</mo>F</mrow>}1101^{3b}{0}^{\mathrm{\infty }},\\ A(a+1,2b+1)& \stackrel{3b^2+12b+5}{\to }& A(a,3b+3).\end{array}$$

Proof

Consider the partial configuration $P(m,n):=01^m\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}01^n{0}^{\mathrm{\infty }}$. The configuration after two steps is $01^{m-1}0\text{<mrow data-mjx-texclass="ORD">A<mo>></mo></mrow>}{1}^{n+1}{0}^{\mathrm{\infty }}$. We note the following shift rule: $$\begin{array}{c}\text{<mrow data-mjx-texclass="ORD">A<mo>></mo></mrow>}{1}^s\stackrel{s}{\to }{1}^s\text{<mrow data-mjx-texclass="ORD">A<mo>></mo></mrow>}\end{array}$$ As a result, we get $01^{m-1}01^{n+1}\text{<mrow data-mjx-texclass="ORD">A<mo>></mo></mrow>}{0}^{\mathrm{\infty }}$ after $n+1$ steps. Advancing two steps produces $01^{m-1}01^{n+2}\text{<mrow data-mjx-texclass="ORD"><mo><</mo>C</mrow>}{0}^{\mathrm{\infty }}$. A second shift rule is useful here: $$\begin{array}{c}{1}^s\text{<mrow data-mjx-texclass="ORD"><mo><</mo>C</mrow>}\stackrel{s}{\to }\text{<mrow data-mjx-texclass="ORD"><mo><</mo>C</mrow>}{1}^s\end{array}$$ This allows us to reach $01^{m-1}0\text{<mrow data-mjx-texclass="ORD"><mo><</mo>C</mrow>}{1}^{n+2}{0}^{\mathrm{\infty }}$ in $n+2$ steps. Moving five more steps gets us to $01^{m-2}\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}01^{n+3}{0}^{\mathrm{\infty }}$, which is the same configuration as $P(m-2,n+3)$. Accounting for the head movement creates the condition that $m\ge 4$. In summary: $$\begin{array}{c}P(m,n)\stackrel{2n+12}{\to }P(m-2,n+3)\text{ if }m\ge 4.\end{array}$$ With $A(a,b)$ we have $P(b,0)$. As a result, we can apply this rule $\lfloor \frac{1}{2}b\rfloor -1$ times (assuming $b\ge 4$), which creates two possible scenarios:

1. If $b\equiv 0(\mathrm{mod}2)$, then in $\sum _{i=0}^{(b/2)-2}(2\times 3i+12)=\frac{3}{4}{b}^2+\frac{3}{2}b-6$ steps we arrive at $P(2,\frac{3}{2}b-3)$. The matching complete configuration is $0^{\mathrm{\infty }}{1}^{a}011\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}01^{(3b)/2-3}{0}^{\mathrm{\infty }}$. After $3b+4$ steps this is $0^{\mathrm{\infty }}{1}^a\text{<mrow data-mjx-texclass="ORD"><mo><</mo>C</mrow>}001^{(3b)/2}{0}^{\mathrm{\infty }}$, which then leads to $0^{\mathrm{\infty }}\text{<mrow data-mjx-texclass="ORD"><mo><</mo>C</mrow>}{1}^{a}001^{(3b)/2}{0}^{\mathrm{\infty }}$ in $a$ steps. After five more steps, we reach $0^{\mathrm{\infty }}1\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}{1}^{a+2}001^{(3b)/2}{0}^{\mathrm{\infty }}$, from which another shift rule must be applied:$$\begin{array}{c}\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}{1}^s\stackrel{s}{\to }{1}^s\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}\end{array}$$Doing so allows us to get the configuration $0^{\mathrm{\infty }}{1}^{a+3}\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}001^{(3b)/2}{0}^{\mathrm{\infty }}$ in $a+2$ steps. In six steps we have $0^{\mathrm{\infty }}{1}^{a+2}011\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}{1}^{(3b)/2}{0}^{\mathrm{\infty }}$, so we use the shift rule again, ending at $0^{\mathrm{\infty }}{1}^{a+2}01^{(3b)/2+2}\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}{0}^{\mathrm{\infty }}$, equal to $A(a+2,\frac{3}{2}b+2)$, $\frac{3}{2}b$ steps later. This gives a total of $2a+\frac{3}{4}{b}^2+6b+11$ steps.
2. If $b\equiv 1(\mathrm{mod}2)$, then in $\frac{3}{4}{b}^2-\frac{27}{4}$ steps we arrive at $P(3,\frac{3b-9}{2})$. The matching complete configuration is $0^{\mathrm{\infty }}{1}^{a}0111\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}01^{(3b-9)/2}{0}^{\mathrm{\infty }}$. After $3b+2$ steps this becomes $0^{\mathrm{\infty }}{1}^a\text{<mrow data-mjx-texclass="ORD"><mo><</mo>F</mrow>}1101^{(3b-3)/2}{0}^{\mathrm{\infty }}$. If $a=0$ then we have reached the undefined F0 transition with a total of $\frac{3}{4}{b}^2+3b-\frac{19}{4}$ steps. Otherwise, continuing for six steps gives us $0^{\mathrm{\infty }}{1}^{a-1}0111\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}{1}^{(3b-3)/2}{0}^{\mathrm{\infty }}$. We conclude with the configuration $0^{\mathrm{\infty }}{1}^{a-1}01^{(3b+3)/2}\text{<mrow data-mjx-texclass="ORD">E<mo>></mo></mrow>}{0}^{\mathrm{\infty }}$, equal to $A(a-1,\frac{3b+3}{2})$, in $\frac{3b-3}{2}$ steps. This gives a total of $\frac{3}{4}{b}^2+\frac{9}{2}b-\frac{1}{4}$ steps.

The information above can be summarized as $$A(a,b)\to \{\begin{array}{ll}A(a+2,\frac{3}{2}b+2)& \text{if }b\ge 2,b\equiv 0(\mathrm{mod}2);\\ 0^{\mathrm{\infty }}\text{<mrow data-mjx-texclass="ORD"><mo><</mo>F</mrow>}1101^{(3b-3)/2}{0}^{\mathrm{\infty }}& \text{if }b\ge 3,b\equiv 1(\mathrm{mod}2),\text{ and }a=0;\\ A(a-1,\frac{3b+3}{2})& \text{if }b\ge 3,b\equiv 1(\mathrm{mod}2),\text{ and }a>0.\end{array}$$ Substituting $b\leftarrow 2b$ for the first case and $b\leftarrow 2b+1$ for the other two yields the final result.

The page Hydra function shows how these rules can be simplified to use that function instead, along with Hydra.

Coding Antihydra's behaviour

Antihydra's relatively simple rules allow one to write a computer program that mimics its behaviour, terminating if and only if Antihydra halts.

Python code

The following Python program is a straightfoward Antihydra simulator using the Hydra function:

# Keeps track of how many odd and even numbers have been encountered
a = 0
# The iterated value
b = 8
# If a < 0 there have been (strictly) more than twice as many odd as even numbers and the program halts
while a != -1:
    # If b is even, add 2 to a so even numbers count twice
    if b % 2 == 0:
        a += 2
    else:
        a -= 1
    # Add the number divided by two (integer division, rounding down) to itself
    b += b//2

Alternative programs

This code can be codegolfed by noting that the change in a is a function of b % 2. Additionally, integer division by two can be replaced with a bitwise logical right shift by one.

a,b=0,8
while a!=-1:
    a+=2-b%2*3
    b+=b>>1

Another insight is that numerical value of 0 functions as the Boolean False and all others are True. The initial value of a would have to change for the program to terminate under the same halting conditions as Antihydra.

a,b=1,8
while a:a+=2-b%2*3;b+=b>>1

Trajectory

11 steps are required to enter the configuration $A(0,4)$ before the rules are repeatedly applied. So far, Antihydra has been simulated to $2^{31}$ rule steps, at which point $b=1073720884$. Here are the first few: $$\begin{array}{c}A(0,4)\stackrel{47}{\to }A(2,8)\stackrel{111}{\to }A(4,14)\stackrel{250}{\to }A(6,23)\stackrel{500}{\to }A(5,36)\stackrel{1209}{\to }A(7,56)\stackrel{2713}{\to }A(9,86)\to \cdots \end{array}$$

A heuristic nonhalting argument

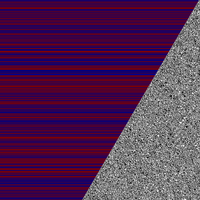
A binary representation of the first 1000 $b$ values, each of which is computed from the previous by the iteration b += b>>1. Rows with blue have even values and rows with red have odd values.

The trajectory of $b$ values can be approximated by a random walk in which the walker can only move in step sizes +2 or -1 with equal probability, starting at position 0. If $P(n)$ is the probability that the walker will reach position -1 from position $n$, then it can be seen that $P(n)=\frac{1}{2}P(n-1)+\frac{1}{2}P(n+2)$. Solutions to this recurrence relation come in the form $P(n)=c_0{\left(\frac{\sqrt{5}-1}{2}\right)}^n+c_1+c_2{(-\frac{1+\sqrt{5}}{2})}^n$, which after applying the appropriate boundary conditions reduces to $P(n)={\left(\frac{\sqrt{5}-1}{2}\right)}^{n+1}$. This means that if the walker were to get to position 1073720884 then the probability of it ever reaching position -1 is ${\left(\frac{\sqrt{5}-1}{2}\right)}^{1073720885}\approx 4.841\times 10^{-224394395}$. This combined with the fact that the expected position of the walker after $k$ steps is $\frac{1}{2}k$ strongly suggests Antihydra probviously runs indefinitely.

To view an animation of the blank tape becoming $A(6,23)$ in 419 steps, click here.