Hydra

Unsolved problem: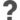

Does Hydra run forever?

1RB3RB---3LA1RA_2LA3RA4LB0LB0LA (bbch)

Hydra is a BB(2,5) Cryptid. Its high-level rules were first reported on Discord by Daniel Yuan on 20 April 2024, who also gave Hydra said name. Later on, a 6-state, 2-symbol Turing machine was discovered and named Antihydra for having similar behaviour to Hydra, making the study of this machine important to the study of that one.

	0	1	2	3	4
A	1RB	3RB	---	3LA	1RA
B	2LA	3RA	4LB	0LB	0LA

The transition table of Hydra.

Analysis

Let $C(a,b):=0^{\infty }\;{\textrm {<A}}\;2\;0^{a}\;3^{b}\;2\;0^{\infty }$. Then,

$${\begin{array}{|lll|}\hline C(2a,0)&\xrightarrow {6a^{2}+20a+4} &0^{\infty }\;3^{3a+1}\;1\;{\textrm {A>}}\;2\;0^{\infty },\\C(2a,b+1)&\xrightarrow {6a^{2}+23a+10} &C(3a+3,b),\\C(2a+1,b)&\xrightarrow {4b+6a^{2}+23a+26} &C(3a+3,b+2).\\\hline \end{array}}$$

Proof

Consider the partial configuration $P(m,n):=0^{\infty }\;3^{m}\;{\textrm {A>}}\;02\;0^{n}$. After 14 steps this configuration becomes $0^{\infty }\;3^{m+3}\;{\textrm {<A}}\;2\;0^{n-2}$. We note the following shift rule:

$${\begin{array}{|c|}\hline 3^{s}\;{\textrm {<A}}\xrightarrow {s} {\textrm {<A}}\;3^{s}\\\hline \end{array}}$$

Using this shift rule, we get $0^{\infty }\;{\textrm {<A}}\;3^{m+3}\;2\;0^{n-2}$ in $m+3$ steps. From here, we can observe that ${\textrm {A>}}\;0\;3^{s}$ turns into $3\;{\textrm {A>}}\;0\;3^{s-1}$ in three steps if $s\geq 1$. By repeating this process, we acquire this transition rule:

$${\begin{array}{|c|}\hline {\textrm {A>}}\;0\;3^{s}\xrightarrow {3s} 3^{s}\;{\textrm {A>}}\;0\\\hline \end{array}}$$

With this rule, it takes $3m+9$ steps to reach the configuration $0^{\infty }\;3^{m+3}\;{\textrm {A>}}\;02\;0^{n-2}$, which is the same configuration as $P(m+3,n-2)$. To summarize:

$${\begin{array}{|c|}\hline P(m,n)\xrightarrow {4m+26} P(m+3,n-2){\text{ if }}n\geq 2.\\\hline \end{array}}$$

With $C(a,b)$ we have $P(0,a)$. As a result, we can apply this rule ${\textstyle {\big \lfloor }{\frac {1}{2}}a{\big \rfloor }}$ times, which creates two possible scenarios:

1. If $a\equiv 0\ (\operatorname {mod} 2)$, then in $\sum _{i=0}^{(a/2)-1}(4\times 3i+26)=\textstyle {\frac {3}{2}}a^{2}+10a$ steps we arrive at ${\textstyle P{\Big (}{\frac {3}{2}}a,0{\Big )}}$. The matching complete configuration is $0^{\infty }\;3^{(3/2)a}\;{\textrm {A>}}\;02\;3^{b}\;2\;0^{\infty }$, which in four steps becomes $0^{\infty }\;3^{(3/2)a+1}\;1\;{\textrm {A>}}\;3^{b}\;2\;0^{\infty }.$ If $b=0$ then we have reached the undefined A2 transition in ${\textstyle {\frac {3}{2}}a^{2}+10a+4}$ steps total. Otherwise, continuing for three steps gives us $0^{\infty }\;3^{(3/2)+2}\;{\textrm {<B}}\;0\;3^{b-1}\;2\;0^{\infty }$. Another shift rule is required here:
   $${\begin{array}{|c|}\hline 3^{s}\;{\textrm {<B}}\xrightarrow {s} {\textrm {<B}}\;0^{s}\\\hline \end{array}}$$
   This means the configuration becomes $0^{\infty }\;{\textrm {<B}}\;0^{(3/2)a+3}\;3^{b-1}\;2\;0^{\infty }$ in ${\textstyle {\frac {3}{2}}a+2}$ steps, and $0^{\infty }\;{\textrm {<A}}\;2\;0^{(3/2)a+3}\;3^{b-1}\;2\;0^{\infty }$, equal to ${\textstyle C{\Big (}{\frac {3}{2}}a+3,b-1{\Big )}}$, one step later. This gives a total of ${\textstyle {\frac {3}{2}}a^{2}+{\frac {23}{2}}a+10}$ steps.
2. If $a\equiv 1\ (\operatorname {mod} 2)$, then in ${\textstyle {\frac {3}{2}}a^{2}+7a-{\frac {17}{2}}}$ steps we arrive at ${\textstyle P{\Big (}{\frac {3a-3}{2}},1{\Big )}}$. The matching complete configuration is $0^{\infty }\;3^{(3a-3)/2}\;{\textrm {A>}}\;020\;3^{b}\;2\;0^{\infty }$, which in four steps becomes $0^{\infty }\;3^{(3a-1)/2}\;1\;{\textrm {A>}}\;0\;3^{b}\;2\;0^{\infty }$, and then $0^{\infty }\;3^{(3a-1)/2}\;1\;3^{b}\;{\textrm {A>}}\;02\;0^{\infty }$ in $3b$ steps. After 14 steps, we see the configuration $0^{\infty }\;3^{(3a-1)/2}\;1\;3^{b+3}\;{\textrm {<A}}\;2\;0^{\infty }$, which turns into $0^{\infty }\;3^{(3a-1)/2}\;1\;{\textrm {<A}}\;3^{b+3}\;2\;0^{\infty }$ in $b+3$ steps. In two steps we get $0^{\infty }\;3^{(3a+1)/2}\;{\textrm {<B}}\;0\;3^{b+2}\;2\;0^{\infty }$, followed by $0^{\infty }\;{\textrm {<B}}\;0^{(3a+3)/2}\;3^{b+2}\;2\;0^{\infty }$ after ${\textstyle {\frac {3a+1}{2}}}$ more steps. We conclude with $0^{\infty }\;{\textrm {<A}}\;2\;0^{(3a+3)/2}\;3^{b+2}\;2\;0^{\infty }$, equal to ${\textstyle C{\Big (}{\frac {3a+3}{2}},b+2{\Big )}}$, one step later. This gives a total of ${\textstyle 4b+{\frac {3}{2}}a^{2}+{\frac {17}{2}}a+16}$ steps.

The information above can be summarized as

$$C(a,b)\rightarrow {\begin{cases}0^{\infty }\;3^{(3/2)a+1}\;1\;{\textrm {A>}}\;2\;0^{\infty }&{\text{if }}a\equiv 0{\pmod {2}}{\text{ and }}b=0,\\C{\Big (}{\frac {3}{2}}a+3,b-1{\Big )}&{\text{if }}a\equiv 0{\pmod {2}}{\text{ and }}b>0,\\C{\Big (}{\frac {3a+3}{2}},b+2{\Big )}&{\text{if }}a\equiv 1{\pmod {2}}.\end{cases}}$$

Substituting $a\leftarrow 2a$ for the first two cases and $a\leftarrow 2a+1$ for the third yields the final result.

In effect, the halting problem for Hydra is about whether repeatedly applying the function $f(n)=3{\Big \lfloor }{\frac {n}{2}}{\Big \rfloor }+3$ will at some point produce more even values of $n$ than twice the number of odd values.

An alternative version of these rules exists that makes the connection to Antihydra more apparent by using the function ${\textstyle H(n)=\left\lfloor {\frac {3}{2}}n\right\rfloor }$, or the Hydra function.

Trajectory

It takes 20 steps to reach the configuration $C(3,0)$, and from there, the Collatz-like rules are repeatedly applied. Simulating Hydra has shown that after 4000000 rule steps, we have $b=2005373$. Here are the first few:

$${\begin{array}{|c|}\hline C(3,0)\xrightarrow {55} C(6,2)\xrightarrow {133} C(12,1)\xrightarrow {364} C(21,0)\xrightarrow {856} C(33,2)\xrightarrow {1938} C(51,4)\xrightarrow {4367} C(78,6)\rightarrow \cdots \\\hline \end{array}}$$

The heuristic argument that suggests Antihydra is a probviously nonhalting machine can be applied here. This means that if $b$ is to be thought of as moving randomly, then the probability of Hydra halting is ${\textstyle {{\Big (}{\frac {{\sqrt {5}}-1}{2}}{\Big )}}^{2005374}\approx 4.168\times 10^{-419099}}$.