Hydra function

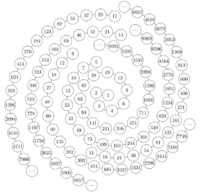
A spiral-like figure that gives the first few terms of the Hydra sequences with initial values 2, 5, 8, 11, and 17.

The Hydra function is a Collatz-like function defined as:

$$\textstyle H(n)\equiv n+\left\lfloor {\frac {1}{2}}n\right\rfloor ={\Big \lfloor }{\frac {3}{2}}n{\Big \rfloor }={\begin{cases}{\frac {3n}{2}}&{\text{if }}n\equiv 0{\pmod {2}},\\{\frac {3n-1}{2}}&{\text{if }}n\equiv 1{\pmod {2}}.\\\end{cases}}$$

It is named as such due its connection to the unsolved halting problems for the Cryptids Hydra and Antihydra. Due to its simplicity, simulations for both of these Turing machines utilize this function instead of what can initially be proven.

Relationship to Hydra and Antihydra

Using the Hydra function, we can obtain simplified rules for Hydra and Antihydra:

Hydra

Antihydra

Let $C_{H}(a,b):=0^{\infty }\;{\textrm {<A}}\;2\;0^{3(a-2)}\;3^{b}\;2\;0^{\infty }$: $${\begin{array}{|lll|}\hline 0^{\infty }\;{\textrm {A>}}\;0^{\infty }&\xrightarrow {20} &C_{H}(3,0),\\C_{H}(2a,0)&\xrightarrow {54a^{2}-48a-2} &0^{\infty }\;3^{9a-8}\;1\;{\textrm {A>}}\;2\;0^{\infty },\\C_{H}(2a,b+1)&\xrightarrow {54a^{2}-39a-5} &C_{H}(3a,b),\\C_{H}(2a+1,b)&\xrightarrow {4b+54a^{2}-3a+4} &C_{H}(3a+1,b+2).\\\hline \end{array}}$$

Let $A_{H}(a,b):=0^{\infty }\;1^{a}\;0\;1^{b-4}\;{\textrm {E>}}\;0^{\infty }$: $${\begin{array}{|lll|}\hline 0^{\infty }\;{\textrm {A>}}\;0^{\infty }&\xrightarrow {11} &A_{H}(0,8),\\A_{H}(a,2b)&\xrightarrow {2a+3b^{2}-1} &A_{H}(a+2,3b),\\A_{H}(0,2b+1)&\xrightarrow {3b^{2}-3b-7} &0^{\infty }\;{\textrm {<F}}\;110\;1^{3b-6}\;0^{\infty },\\A_{H}(a+1,2b+1)&\xrightarrow {3b^{2}-7} &A_{H}(a,3b+1).\\\hline \end{array}}$$

Proof

Recall the high-level rules for Hydra and Antihydra:

Hydra

Antihydra

Let $C(a,b):=0^{\infty }\;{\textrm {<A}}\;2\;0^{a}\;3^{b}\;2\;0^{\infty }$: $${\begin{array}{|lll|}\hline 0^{\infty }\;{\textrm {A>}}\;0^{\infty }&\xrightarrow {20} &C(3,0),\\C(2a,0)&\xrightarrow {6a^{2}+20a+4} &0^{\infty }\;3^{3a+1}\;1\;{\textrm {A>}}\;2\;0^{\infty },\\C(2a,b+1)&\xrightarrow {6a^{2}+23a+10} &C(3a+3,b),\\C(2a+1,b)&\xrightarrow {4b+6a^{2}+23a+26} &C(3a+3,b+2).\\\hline \end{array}}$$

Let $A(a,b):=0^{\infty }\;1^{a}\;0\;1^{b}\;{\textrm {E>}}\;0^{\infty }$: $${\begin{array}{|lll|}\hline 0^{\infty }\;{\textrm {A>}}\;0^{\infty }&\xrightarrow {11} &A(0,4),\\A(a,2b)&\xrightarrow {2a+3b^{2}+12b+11} &A(a+2,3b+2),\\A(0,2b+1)&\xrightarrow {3b^{2}+9b-1} &0^{\infty }\;{\textrm {<F}}\;110\;1^{3b}\;0^{\infty },\\A(a+1,2b+1)&\xrightarrow {3b^{2}+12b+5} &A(a,3b+3).\\\hline \end{array}}$$

Already, both machines appear to have very similar functions. They have one parameter that increases exponentially with growth factor ${\textstyle {\frac {3}{2}}}$ and another that effectively takes a pseudo-random walk. Below, the exponentially increasing variables are described by integer sequences:

Hydra	Antihydra
$$a_{0}=3,a_{n+1}={\begin{cases}{\frac {3a_{n}+6}{2}}&{\text{if }}a_{n}\equiv 0{\pmod {2}}\\{\frac {3a_{n}+3}{2}}&{\text{if }}a_{n}\equiv 1{\pmod {2}}\end{cases}}$$	$$a_{0}=4,a_{n+1}={\begin{cases}{\frac {3a_{n}+4}{2}}&{\text{if }}a_{n}\equiv 0{\pmod {2}}\\{\frac {3a_{n}+3}{2}}&{\text{if }}a_{n}\equiv 1{\pmod {2}}\end{cases}}$$

This makes illustrating the transformation easier. Now we will define a new integer sequence based on the old one and discover the recursive rules for that sequence. This new sequence is ${\textstyle b_{n}={\frac {1}{3}}a_{n}+2}$ and $b_{n}=a_{n}+4$ for Hydra and Antihydra respectively. We start by using $b_{n+1}$ instead and substituting $a_{n+1}$ for its recursive formula. By doing so, we get:

Hydra	Antihydra
$$b_{0}=3,b_{n+1}={\begin{cases}{\frac {a_{n}+6}{2}}&{\text{if }}a_{n}\equiv 0{\pmod {2}}\\{\frac {a_{n}+5}{2}}&{\text{if }}a_{n}\equiv 1{\pmod {2}}\end{cases}}$$	$$b_{0}=8,b_{n+1}={\begin{cases}{\frac {3a_{n}+12}{2}}&{\text{if }}a_{n}\equiv 0{\pmod {2}}\\{\frac {3a_{n}+11}{2}}&{\text{if }}a_{n}\equiv 1{\pmod {2}}\end{cases}}$$

After that, we can substitute $a_{n}$ for its solution in terms of $b_{n}$. What results is the following:

Hydra	Antihydra
$$b_{0}=3,b_{n+1}={\begin{cases}{\frac {3(b_{n}-2)+6}{2}}&{\text{if }}3(b_{n}-2)\equiv 0{\pmod {2}}\\{\frac {3(b_{n}-2)+5}{2}}&{\text{if }}3(b_{n}-2)\equiv 1{\pmod {2}}\end{cases}}$$	$$b_{0}=8,b_{n+1}={\begin{cases}{\frac {3(b_{n}-4)+12}{2}}&{\text{if }}b_{n}-4\equiv 0{\pmod {2}}\\{\frac {3(b_{n}-4)+11}{2}}&{\text{if }}b_{n}-4\equiv 1{\pmod {2}}\end{cases}}$$

We note that the if statements simplify to checking if $b_{n}$ is even or odd. After simplifying, we are done:

Hydra	Antihydra
$$b_{0}=3,b_{n+1}={\begin{cases}{\frac {3b_{n}}{2}}&{\text{if }}b_{n}\equiv 0{\pmod {2}}\\{\frac {3b_{n}-1}{2}}&{\text{if }}b_{n}\equiv 1{\pmod {2}}\end{cases}}$$	$$b_{0}=8,b_{n+1}={\begin{cases}{\frac {3b_{n}}{2}}&{\text{if }}b_{n}\equiv 0{\pmod {2}}\\{\frac {3b_{n}-1}{2}}&{\text{if }}b_{n}\equiv 1{\pmod {2}}\end{cases}}$$

Now that we have demonstrated a strong similarity in the behaviour of both Turing machines, we can return to using the high-level rules. Doing that while accounting for the step counts yields the final result.

Properties

The Hydra function can be rewritten as follows:

$${\begin{array}{l}H(2n)&=&3n,\\H(2n+1)&=&3n+1.\\\end{array}}$$

Now we will define $s$ and $t$ to be positive integers with $t$ additionally being odd, and substitute $n\leftarrow 2^{s-1}t$:

$${\begin{array}{l}H(2^{s}t)&=&2^{s-1}\times 3t,\\H(2^{s}t+1)&=&2^{s-1}\times 3t+1.\\\end{array}}$$

Because $2^{s-1}\times 3t$ is also the result of substituting $s\leftarrow s-1$ and $t\leftarrow 3t$, we can iterate the Hydra function many times. Letting $H^{k}(n)=\underbrace {H(\cdots (H(H(n)))\cdots )} _{k{\text{ times}}}$, this means:

$${\begin{array}{l}H^{s}(2^{s}t)&=&3^{s}t,\\H^{s}(2^{s}t+1)&=&3^{s}t+1.\\\end{array}}$$

This optimization can be directly applied to the high-level rules for Hydra and Antihydra, producing this result:

Hydra	Antihydra
Let $C_{H}(a,b):=0^{\infty }\;{\textrm {<A}}\;2\;0^{3(a-2)}\;3^{b}\;2\;0^{\infty }$: $${\begin{array}{|lll|}\hline C_{H}(2^{s}t,b+s)&\rightarrow &C_{H}(3^{s}t,b),\\C_{H}(2^{s}t+1,b)&\rightarrow &C_{H}(3^{s}t+1,b+2s),\\\hline \end{array}}$$	Let $A_{H}(a,b):=0^{\infty }\;1^{a}\;0\;1^{b-4}\;{\textrm {E>}}\;0^{\infty }$: $${\begin{array}{|lll|}\hline A_{H}(a,2^{s}t)&\rightarrow &A_{H}(a+2s,3^{s}t),\\A_{H}(a+s,2^{s}t+1)&\rightarrow &A_{H}(a,3^{s}t+1),\\\hline \end{array}}$$