1RB1RE_1LC0RA_0RD1LB_---1RC_1LF1RE_0LB0LE

1RB1RE_1LC0RA_0RD1LB_---1RC_1LF1RE_0LB0LE (bbch)

Unsolved problem:

Does this TM run forever?

A holdout BB(6) TM discovered by @-d on 25 Jun 2024 which is modeled by

A(a, b) -> A(a-b, 4b+2) if a > b
A(a, b) -> A(2a+1, b-a) if a < b
A(a, b) -> Halt if a = b

Start A(1, 2)

for A(a, b) = 0^inf 10^{a-1} 0 1^b E> 0^inf. The configuration is always valid because $a\geq 1$ is always maintained. Forward simulations of this model by @-d and Andrew Ducharme do not halt after 100,000,000 iterations of the map A(a,b). It is the inspiration for the Beaver Math Olympiad.

Relation to Other Math Problems

This TM is a possible Cryptid since it seems hard to predict whether we could ever end up in A(n, n). However, it is not (yet) classified as a Cryptid because there are no arguments for why this TM is hard (e.g., by comparing it to an open/unsolved/hard mathematical problem).

The map A(., .) is related to the study of discontinuous dynamical systems. When +2 and +1 are ignored, the value of $\ln(a/b)$ follows this chaotic map:

$$F(x)={\begin{cases}\ln \left({\frac {e^{x}-1}{4}}\right)&{\text{if }}x>0\\\ln \left({\frac {2}{e^{-x}-1}}\right)&{\text{if }}x<0\end{cases}}$$

This map F(.) is related to the study of discontinuous dynamical systems.

A Backward Reasoning Approach

An alternative approach is to work backwards and study the points which A(a,b) maps to the line a = b. For example, the points (2,7), (3,25), (4,71), and (5,181) all eventually map to a = b. (2,7) is immediately sent to a = b because, under the a < b rule,

$$A(2,7)=(4+1,7-2)=(5,5)$$

(5,181) requires more steps:

$$(5,181)\rightarrow (11,176)\rightarrow (23,165)\rightarrow (47,142)\rightarrow (95,95)$$

How are these points found? It's faster not to consider individual points, but as @Rae identified, the set of lines which are mapped to a = b. Introducing an index $n$, we can rewrite A(a,b) as

$$(x_{n+1},y_{n+1})={\begin{cases}(x_{n}-y_{n},4y_{n}+2),&{\text{if }}x_{n}\geq y_{n}\\(2x_{n}+1,y_{n}-x_{n}),&{\text{if }}x_{n}<y_{n}\end{cases}}$$

If $x_{n+1}=y_{n+1}$, then the lines with slopes $y_{n+1}=mx_{n+1}+b$ map to that line. The two possible slopes are, for $x_{n}>y_{n}$and $x_{n}<y_{n}$ respectively,

$4y_{n}+2=m(x_{n}-y_{n})+b\iff y_{n}={\frac {m}{m+4}}x_{n}+{\frac {b-2}{m+4}}$ and$y_{n}-x_{n}=m(2x_{n}+1)+b\iff y_{n}=(2m+1)x_{n}+(b+m).$

Indexing m and b themselves, in (slope, y-intercept) space,

$(m_{k-1},b_{k-1})={\begin{cases}\left({\frac {m_{k}}{m_{k}+4}},{\frac {b_{k}-2}{m_{k}+4}}\right),&x_{k-1}>y_{k-1}\\(2m_{k}+1,b_{k}+m_{k}),&x_{k-1}<y_{k-1}\end{cases}}$.

Iteratively applying this (m,b) map finds an infinite set of points which A sends to a = b. The starting point is said line, with (m, b) = (1,0). Then the two lines of points which map to points on the line (m,b) = (1,0) under a single application A are have slopes and y-intercepts of $\left({\frac {1}{5}},-{\frac {2}{5}}\right)=\left({\frac {1}{1+4}},{\frac {0-2}{1+4}}\right)$ and (3,1) = (2 + 1, 0 + 1). The four lines of points which map to (1,0) under two applications of A have slopes and y-intercepts $\left({\frac {1}{21}},-{\frac {4}{7}}\right),\left({\frac {7}{5}},-{\frac {1}{5}}\right),\left({\frac {3}{7}},-{\frac {1}{7}}\right)$ and (7,4).

Each point in the plotted (slope, intercept) space represents a line of points in (x,y) space that are eventually mapped to y = x by iterated application of the operation A. These points require five or fewer iterations to do so.

Each plotted point in (slope, intercept) space represents a line of points in (x,y) space which is mapped to y = x by nine or fewer iterated applications of A. If any point is on the black line, the TM in question halts.

To apply this to the problem at hand, we want to know if any of these generated lines contain the point (1,2), our TM-derived initial condition. The set of all lines (in position space, or (x,y) space) containing (1,2) are described by the line in (m,b) space 2 = m + b. If any of the generated points in (m,b) space sit on 2 = m + b, then the point (x,y) = (1,2) is eventually mapped by A to a point where x = y. In the second image, of (m,b) points after nine iterations, we see there are three possible locations for this to occur.

Each plotted point in (slope, intercept) space represents a line of points in (x,y) space which is mapped to y = x by ten or fewer iterated applications of A, with m > 2 and b > 0. If any point is on the black line, the TM in question halts. There are three possible locations. Two do not hit the line (in finite time). The third's status is unknown.

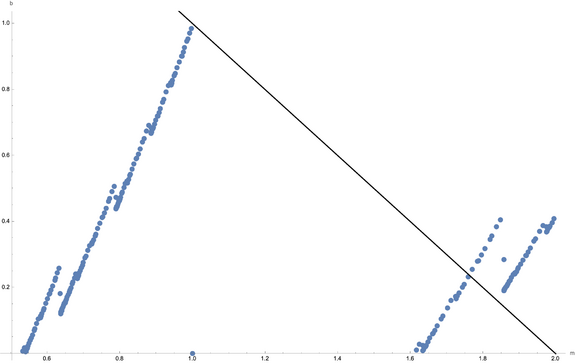
Location 1: Approaching (m = 1, b= 1) from below

There's two ways to see how (1,1) is not actually an intersection point. First, from Rae, the elementary one: if m > b, m will always be greater than b, so a point where m = b is impossible.

Second, from Andrew, if one wants to generate a point near m = 1, you should create the largest possible value M to swamp out the additive +4 in the denominator of M/(M+4). M can be maximized with n iterations of the (m,b) map by only using the x < y operation. Then apply the x > y operation once for a near-unitary slope. The pair $(m_{n},b_{n})$ formed by applying the x < y operation n times to (1,0) is $(2^{n+1}-1,2^{n+1}-n-2)$. Apply the x > y operation to get

$\left({\frac {2^{n+1}-1}{2^{n+1}+3}},{\frac {2^{n+1}-n-4}{2^{n+1}+3}}\right)$.

Taking the limit as n goes to infinity, we get (1,1), so this TM does not reach the line 2 = m + b here in finite time.

Location 2: Approaching (m = 13/7, b = 4/21) from above

The rightmost possible intersection is the least likely: its approach towards 2 = m + b slows considerably with increasing iterations (because its limit will end up being to above this line). Empirically examining these points, they appear to be near (1.85, 0.19). After 6 through 9 iterations, the closest of the generated (m,b) points to (1.85, 0.19) are (285/151, 37/151), (1117/599, 123/599), (4445/2391, 155/797), and (17757/9559, 1831/9559). Such points are formed by n applications of the (m,b) map when x > y, then two applications of the (m,b) map when x < y, then a single additional application of the x > y and x < y (m,b) maps, in that order. A more concise notation would be $(>^{n},<^{2},>,<)$.

A closed form equation in n for $(>^{n},<^{2},>,<)$ starting from (1,0) is $\left({\frac {13*4^{n+1}+23}{7*4^{n+1}+5}},{\frac {4^{n+2}+6n+65}{21*4^{n+1}+15}}\right)$. Its limit as $n\rightarrow \infty$ is $\left({\frac {13}{7}},{\frac {4}{21}}\right)$, which is safely above 2 = m + b. This strand of points will never cause a halting condition.

Rae showed the same by applying the bounds m > 0 and $b>-{\frac {2}{3}}$ on the sequence $(<^{2},>,<)$:

${\begin{aligned}m_{0}>0,b_{0}>-{\frac {2}{3}}&\implies m_{1}>1,b_{1}>-{\frac {2}{3}}\\&\implies m_{2}>3,b_{2}>{\frac {1}{3}}\\&\implies m_{3}>{\frac {3}{7}},b_{3}>-{\frac {5}{21}}\\&\implies m_{4}>{\frac {13}{7}},b_{4}>{\frac {4}{21}}\end{aligned}}$

Since the combination of operations is empirically determined, this isn't strictly a proof, but the moderate distance of these points from 2 = m + b means the burden of proof isn't that high.

Location 3: Jumping above and below b = 2 - m around m = 1.76...infinitely?

Notes from my (Andrew) analysis, from when I tried to repeat looking at the points closest to the not-quite-intersection of the sparse set and line b = 2 - m. I went 25 iterations of the slope map before realizing it was likely a fractal and zooming in would give me more of the same:

Slopes of points (m,b) closest to the line m = 2 - b from above and below

13/7 for n = 5 is above and to the right, 119/69 for n = 6 is below and to the left, 223/125 for n = 7 is above and to the right, 669/401 for n = 8 is below left. 
Things start to get more complicated at n = 9, as the doubling of dots becomes a little overwhelming.
So many dots at n = 13 you have to zoom in
n = 9 above:  223/125, n = 9 below: 1145/651
n = 10 above: 2037/1151, n = 10 below: 1145/651 (still)
n = 11 above: 6617/3755, n = 11 below: 1145/651 (still)
n = 12 above: 6617/3755 (still), n = 12 below: 24937/14171
n = 13 above: 6617/3755 (still), n = 13 below: 38171/21681
n = 14 above: 6617/3755 (still), n = 14 below: 64639/36701
n = 15 above: 117575/66741,     n = 15 below: 64639/36701 (still)
n = 16 above: 117575/66741 (still), n = 16 below: 376131/213545
n = 17 above: 611281/347027,        n = 17 below: 376131/213545 (still). 
b for the new point here is 2 / 347027 from being on the line!!
At n = 17, have we crossed the Rubicon? This super close point is just above the line, so is anything new now above it?
No! yowza.
n = 18 above: 611281/347027 (still), n = 18 below: 611281/347027.
n = 19 above: 611281/347027 (still), n = 19 below: 2115805/1201207
n = 20 above: 611281/347027 (still), n = 20 below: 3338367/1895261
n = 21 above:611281/347027 (still) , n = 21 below: 10673739/6059585 
There's a new point next to our hero which is just to the right and just above. Above trend hitting limit point?
NO!!
n = 22 above: 208917121/118603171, n = 22 below: 20454235/11612017 I might be seeing a new trend line forming
n = 23 above: 834868865/473958819, n = 23 below: 40015227/22716881
n = 24 above: 3338675841/1895381411, n = 24 below: 40015227/22716881 (still)
n = 25 above: 79137211/44926609,     n = 25 below: 239198119/135794133


I think I'm zooming in on a fractal structure and will never see the end of this.

To demonstrate the fractal, the generated (m,b) set after n iterations for n = 9, n = 15, n = 20, and n = 25. Note the change in scale on the horizontal and vertical axes. I'm roughly specifying another decimal place in the axes bounds as I look at smaller and smaller region. Largely a copy of post @aducharme July 27th, 2024 10:24 PM PT

Unless we actually hit the halting condition, we can generate an infinite number of blue points arbitrarily close to the yellow line from both above and below.

It does appear that points within roughly the range 1.724 < m < 1.8556 are generated from finding all possible combinations of operations > and < after n applications, then applying $(<,<,<,>,<,>,<)=(<^{4},(>,<)^{2})=(<^{4},>,<,>,<)$. This is equivalent to

$$(m_{f},b_{f})=\left({\frac {104m_{n}+119}{56m_{n}+69}},{\frac {23m_{n}+b_{n}+12}{56m_{n}+69}}\right).$$

Study of Simplified Model

@savask 06/26/2024 11:54 PM

Maybe we could tackle a simplified version of this problem? For example, let's remove the constant terms:

(a, b) -> (a-b, 4*b) if a > b
(a, b) -> (2*a, b-a) if b > a
(a, b) -> Halt if a = b

And let's start from config (3,17), since it appears in the run of the original machine.

The average increase in $\ln a$ is

${\frac {-{\frac {\pi ^{2}}{12}}+3{\frac {(\ln 2)^{2}}{2}}+{\text{Li}}_{2}(1/4)}{\ln 3}}\approx 0.15097694$

when modeled from the PDF

$f(r)={\frac {2}{\ln 3(r+1)(r+3)}}$

in $r=b/a$, as found by @LegionMammal978 and Math.SE user "Sil".

Note that the simplified iteration trivially cannot halt as written: after 2 steps, it reaches $(12,8)$ and becomes trapped within the families $(a,b)\equiv (0,4)$ and $(a,b)\equiv (4,0){\pmod {8}}$.

Development of Model from TM Tape

@-d 25 Jun 2024 2:29 AM ET:

Let f(a,b) represent (10)^a D> 1^b. By inspection, the machine visits f(0,3) f(2,2) f(1,7) f(4,5) f(0,19) f(2,18) f(6,15) f(14,8).

I got these rules for f(a,b) and verified them up to 0<=a<=100 and 1<=b<=100.
f(a,b) -> f(a-b+1,4b-1) if b < a+2
f(a,a+2) -> halt
f(a,b) -> f(2a+2,b-a-1) if b > a+2


I ran these rules from f(0,3) and gave up after reaching a,b > 2^1000000. It looks like halting becomes less and less likely. Is there a way to show this runs forever (or miraculously halts)?

@Shawn Ligocki — 25 Jun 2024 at 11:56 PM ET:

I can confirm roughly the same rules (I chose a slightly different standard config):
1RB1RE_1LC0RA_0RD1LB_---1RC_1LF1RE_0LB0LE

E(a, b, c)  =  0^inf 10^a 0 10^b 1^c E> 0^inf

Base Rules:
  E(a+1, b, c+2) -> E(a, b+2, c+1)
  E(a+1, b, 1)   -> E(a, 0, 2b+6)
  E(0,   b, c+2) -> E(b+2, 0, c+1)
  E(0,   b, 1)   -> Halt(b+4)

High-level Rules:
  E(a, 0, c+1)  -->  E(a-c-1, 0, 4c+6)  if a > c
  E(a, 0, c+1)  -->  E(2a+2, 0, c-a)    if a < c
  E(a, 0, c+1)  -->  Halt(2c+4)         if a = c


Connecting to your notation @-d : f(a, b+2) -> E(a, 0, b+1) 

@Shawn Ligocki — 26 Jun 2024 at 12:25 AM

Hm, this is interesting. I decided to track "spread" akin to what @savask and I have been looking at for the similar 3x3 TM we're looking at in ⁠bbxy . Here I define spread = abs(a - c) in config E1(a, c) = E(a, 0, c+1). Here's the results I have so far:
          1  E1(2, 0) spread: [2, 2] (0.06s)
    100_001  E1(10^6_557, 10^6_555) spread: [1, 10^6_557] (0.44s)
    200_001  E1(10^13_124, 10^13_125) spread: [10^6_557, 10^13_125] (1.27s)
    300_001  E1(10^19_670, 10^19_669) spread: [10^13_123, 10^19_670] (2.52s)
    400_001  E1(10^26_235, 10^26_237) spread: [10^19_668, 10^26_237] (4.23s)
    500_001  E1(10^32_799, 10^32_799) spread: [10^26_235, 10^32_799] (6.39s)
    600_001  E1(10^39_350, 10^39_352) spread: [10^32_799, 10^39_352] (8.98s)
    700_001  E1(10^45_930, 10^45_930) spread: [10^39_350, 10^45_930] (12.06s)
    800_001  E1(10^52_486, 10^52_486) spread: [10^45_929, 10^52_486] (15.54s)
    900_001  E1(10^59_046, 10^59_047) spread: [10^52_485, 10^59_047] (19.57s)
  1_000_001  E1(10^65_613, 10^65_612) spread: [10^59_045, 10^65_613] (24.05s)
  1_100_001  E1(10^72_154, 10^72_153) spread: [10^65_609, 10^72_154] (28.92s)
  1_200_001  E1(10^78_728, 10^78_729) spread: [10^72_153, 10^78_729] (34.21s)
  1_300_001  E1(10^85_288, 10^85_289) spread: [10^78_729, 10^85_289] (40.03s)
  1_400_001  E1(10^91_830, 10^91_829) spread: [10^85_288, 10^91_829] (46.40s)
  1_500_001  E1(10^98_394, 10^98_393) spread: [10^91_829, 10^98_394] (53.11s)
  1_600_001  E1(10^104_961, 10^104_959) spread: [10^98_393, 10^104_961] (60.18s)
  1_700_001  E1(10^111_523, 10^111_523) spread: [10^104_958, 10^111_523] (67.75s)
  1_800_001  E1(10^118_088, 10^118_088) spread: [10^111_523, 10^118_088] (75.77s)
  1_900_001  E1(10^124_631, 10^124_630) spread: [10^118_088, 10^124_631] (84.39s)
  2_000_001  E1(10^131_185, 10^131_185) spread: [10^124_630, 10^131_185] (93.41s)
...
  3_000_001  E1(10^196_733, 10^196_733) spread: [10^190_163, 10^196_733] (217.87s)

Here spread: [X, Y] means that the spread values (since last print) had min X, max Y
So notice that the spread is basically uniformly increasing. In fact these [X, Y] intervals hardly even overlap!
That makes me think there's something about this that makes small spread impossible (and thus halt impossible)
Or that it's like Bigfoot and it ... could go back to zero, but the chances are infinitesimal!

savask — 26 Jun 2024 at 1:02 AM

Maybe we can simplify a little bit more. Set (a, c) = E(a, 0, c+1) then the rules are
(a, c) -> (a-c-1, 4c+5) if a > c
(a, c) -> (2a+2, c-a-1) if a < c
(a, c) -> Halt if a = c

I like that this way they are more symmetrical with a-c-1 vs c-a-1

Shawn Ligocki — 26 Jun 2024 at 2:33 AM

FWIW, there is a value x ~= 1.76 such that as c -> inf: (xc, c) -> (xyc, yc) via path "rll" (right->0 [ie a > c], left->0 [ie a < c], left->0). Which would repeat forever if it were exact, but it is an unstable cycle so any slight deviation and it gets further and further away, so that doesn't seem like a reasonable proof direction :/

dyuan01 — 26 Jun 2024 at 2:32 PM

If we let A(a, c) = (a-1, c-1), we can get these rules:
```
A(a, c) -> A(a-c, 4c+2) if a > c
A(a, c) -> A(2a+1, c-a) if a < c
A(a, c) -> Halt if a = c
```
And we start with (1, 2)

I'm not sure if it even helps, but at least the rules look slightly more "human-manageable"