Tree Rewriting System
What is a Tree-Rewriting System?
A Tree-Rewriting System (TRS for short) is a computational model that defines a transformation between hierarchical structures (trees, often representing terms or code) by repeatedly applying a set of specified rewrite rules.
Definition
We define an alphabet Σ={a,b,(f,f’,f’’,…)}. We can define terms built from these symbols as follows:
- a is a leaf node (constant),
- b is a leaf node (constant),
- f() is a unary function (has 1 child),
- f’() is a binary function (has 2 children),
- f’’() is a ternary function (has 3 children),
…
and so on…
…
In general, f’’…’’() (with n total apostrophes) is an (n+1)-ary function (has n+1 children)
NOTE: each function symbol specifies its arity.
Examples of Valid Trees and Their Graphs
a (single root note labelled a),
f(a) (an unlabelled root with a child a),
f’’(a,f(a),b) (an unlabelled root with three children. The middle child (unlabelled) has a child labelled a,
f’(a,b) (an unlabelled root with two children labelled a and b),
b (single root note labelled b),
f’’’(f’(a,b),b,b,a) (an unlabelled root with four children, the first child has two children a and b. The other three children of the root are labelled b,b, and a.
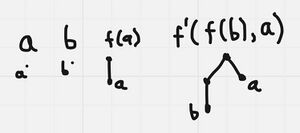
Rulesets in Tree-Rewriting Systems
We consider τ to be an initial valid tree.
A deterministic tree-rewriting systems ruleset R consists of pairs of trees (L→R) where the leftmost instance of L (in τ) is replaced with R. We allow duplicate rules in the same ruleset, and rules are followed in cyclic order (initially rule 1).
If a rule does not apply, simply skip it and move to the immediate next one in R. Skipping a single rule counts as one step.
When Does Halting Occur?
We can say that halting occurs in one of the two following scenarios:
τ has been reduced to a single constant,
or,
There does not exist a rule in R that can further transform τ.
The Tree-Rewriting System In Action
Example 1:
τ: f’(a,f(b))
R: a->b, b->f(a), f’(a,b)->b
f’(a,f(b))
f’(b,f(b)) (as per rule 1)
f’(f(a),f(b)) (as per rule 2)
Skip rule 3
f’(f(b),f(b)) (as per rule 1)
f’(f(f(a)),f(b)) (as per rule 2)
Skip rule 3
f’(f(f(b)),f(b)) (as per rule 1)
f’(f(f(f(a))),f(b)) (as per rule 2)
Skip rule 3
…
This example does not halt.
Example 2:
τ: f’(f(a),f(b))
R: a->f’(a,b), f(b)->b, f(a)->f(b)
f’(f(a),f(b))
f’(f(f’(a,b),f(b)) (as per rule 1)
f’(f(f’(a,b),b)) (as per rule 2)
Skip rule 3
f’(f(f’(f’(a,b),b),b)) (as per rule 1)
Skip rule 2
Skip rule 3
f’(f(f’(f’(f’(a,b),b),b),b)) (as per rule 1)
Skip rule 2
Skip rule 3
f’(f(f’(f’(f’(f’(a,b),b),b),b),b)) (as per rule 1)
…
This example also does not halt.
Functions
From here, we can define a multitude of functions analogous to the classic Busy Beaver. We say that a “size-n tree” consists of n total nodes. Examples include: f(a) (contains two nodes), a (or b) (contains one node), … etc …
BBrw(n)
“The maximum number of steps before halting, taken over all initial trees τ of size ≤n and all rulesets of size ≤n, with each rule part (L→R) also having size ≤n.” (We assume that each rule part can have different lengths (but must be ≤n))
BBlt(n)
“The largest tree size reached before BBrw(n) halts”
BBln(n)
“BBrw(n) but with n total distinct leaf nodes allowed in its alphabet Σ”
Bounds For Small n
BBrw(1)=1 because we can only consider τ=a or b, with a single rule being a->a (infinite loop), b->b (loop), a->b (halt after one step), and b->a (halt after one step). Max(1,1)=1 (non-halters are discarded).