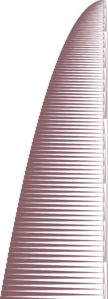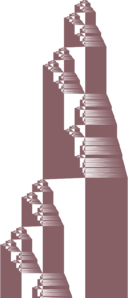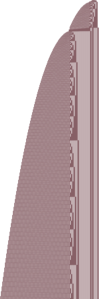Non-halting Turing machine: Difference between revisions
Added links |
Added some more pictures |
||
| Line 92: | Line 92: | ||
!Count | !Count | ||
!Notes and Notable examples | !Notes and Notable examples | ||
!Example space-time diagram | |||
|- | |- | ||
|[[Translated cycler]] | |[[Translated cycler]] | ||
| Line 99: | Line 100: | ||
* {{TM|1RB1LC_0LA1RD_0RB0LC_1LA0RD}}, the current preperiod record holder, with a preperiod of 119,120,230,102. Before phasing into a translated cycle, this machine appears to be a [[spaghetti]]. | * {{TM|1RB1LC_0LA1RD_0RB0LC_1LA0RD}}, the current preperiod record holder, with a preperiod of 119,120,230,102. Before phasing into a translated cycle, this machine appears to be a [[spaghetti]]. | ||
* {{TM|1RB1RC_1LC0RA_0LB0LD_1LA1LD}} starts out as an irregular bell, but phase transitions into a translated cycler with period 4222 at step 29754825. | * {{TM|1RB1RC_1LC0RA_0LB0LD_1LA1LD}} starts out as an irregular bell, but phase transitions into a translated cycler with period 4222 at step 29754825. | ||
| | |||
|- | |- | ||
|[[Cycler]] | |[[Cycler]] | ||
| Line 105: | Line 107: | ||
* {{TM|1RB0RB_1LC0RD_1LA1LB_0LC1RD}}, likely period record holder, with a period of 120. | * {{TM|1RB0RB_1LC0RD_1LA1LB_0LC1RD}}, likely period record holder, with a period of 120. | ||
* {{TM|1RB1LB_1LC1RD_1LA0RD_0LA0RB}}, likely preperiod record holder, with a preperiod of 146. | * {{TM|1RB1LB_1LC1RD_1LA0RD_0LA0RB}}, likely preperiod record holder, with a preperiod of 146. | ||
| | |||
|- | |- | ||
|[[Bouncer]] | |[[Bouncer]] | ||
| Line 112: | Line 115: | ||
* {{TM|1RB0RC_0RC0RB_1LC0LD_1LA0RA}}, starts out as irregular-side bells before phasing into a bouncer at step 3350. | * {{TM|1RB0RC_0RC0RB_1LC0LD_1LA0RA}}, starts out as irregular-side bells before phasing into a bouncer at step 3350. | ||
* {{TM|1RB1LC_0RD0LC_1LB0LA_1LD1RA}}, a bouncer with very complex runs. Start step 145,729. | * {{TM|1RB1LC_0RD0LC_1LB0LA_1LD1RA}}, a bouncer with very complex runs. Start step 145,729. | ||
| | |||
|- | |- | ||
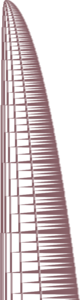
|[[Counter]] | |[[Counter]] | ||
| Line 129: | Line 133: | ||
* {{TM|1RB1LC_0RD0RB_1LA0LA_1LD0LA}}, an example of a superexponential counter. | * {{TM|1RB1LC_0RD0RB_1LA0LA_1LD0LA}}, an example of a superexponential counter. | ||
| | |||
|- | |- | ||
|[[Bell]] | |[[Bell]] | ||
| Line 137: | Line 142: | ||
* {{TM|1RB0LC_1RC1RB_1LA1LD_0RA0RB}}, a grow-and-shrink bell. | * {{TM|1RB0LC_1RC1RB_1LA1LD_0RA0RB}}, a grow-and-shrink bell. | ||
* {{TM|1RB0RC_1LC0RA_1RA1LD_0LC0LA}}, starts out as an irregular bell before phasing into a bell. | * {{TM|1RB0RC_1LC0RA_1RA1LD_0LC0LA}}, starts out as an irregular bell before phasing into a bell. | ||
| | |||
|- | |- | ||
|[[Cubic bell]] | |[[Cubic bell]] | ||
| Line 143: | Line 149: | ||
* {{TM|1RB1RC_1LC0RC_0RA1LD_0LC0LB}}, a cubic inverted bell. | * {{TM|1RB1RC_1LC0RC_0RA1LD_0LC0LB}}, a cubic inverted bell. | ||
* {{TM|1RB0RC_0LD0RA_0LA1RC_1LA1LD}}, a cubic grow-and-shrink bell. | * {{TM|1RB0RC_0LD0RA_0LA1RC_1LA1LD}}, a cubic grow-and-shrink bell. | ||
| | |||
|- | |- | ||
|Bouncer + X | |Bouncer + X | ||
| Line 153: | Line 160: | ||
* {{TM|1RB1LB_0LC0RD_0RA1LC_1RA1RD}}, a bouncer + cubic bell, leading to quartic tape growth on the left. | * {{TM|1RB1LB_0LC0RD_0RA1LC_1RA1RD}}, a bouncer + cubic bell, leading to quartic tape growth on the left. | ||
* {{TM|1RB0LC_1LA1RD_1RA1LD_0LA0RB}}, a bouncer + unclassified. (If you can classify it, let me know in the talk page!) | * {{TM|1RB0LC_1LA1RD_1RA1LD_0LA0RB}}, a bouncer + unclassified. (If you can classify it, let me know in the talk page!) | ||
|<div class="text-align: center">[[File:1RB0LB 1LC1RA 1RD0LC 0LA0RB.png|frameless|300x300px]]</div> | |||
|- | |- | ||
| | |Bounce-counter | ||
|≈330 | |≈330 | ||
| | | | ||
* {{TM|1RB1LC_1LC0RB_1RA0LD_1RA1LA}}, a typical | * {{TM|1RB1LC_1LC0RB_1RA0LD_1RA1LA}}, a typical binary bounce-counter. | ||
* {{TM|1RB1LB_1RC1RD_0LA0RC_1LD0LB}}, a typical | * {{TM|1RB1LB_1RC1RD_0LA0RC_1LD0LB}}, a typical quaternary bounce-counter. | ||
* {{TM|1RB1RA_0RC0LC_1LA0LD_0RA1LC}}, a | * {{TM|1RB1RA_0RC0LC_1LA0LD_0RA1LC}}, a ternary bounce-counter, which is more rare. | ||
* {{TM|1RB0LA_0RC1LA_0RD1RB_1LD1LA}}, a hybrid quaternary-octal | * {{TM|1RB0LA_0RC1LA_0RD1RB_1LD1LA}}, a hybrid quaternary-octal bounce-counter. | ||
* {{TM|1RB0LC_1RD0RB_1LA1RC_1LC1RB}}, a | * {{TM|1RB0LC_1RD0RB_1LA1RC_1LC1RB}}, a 3/2-bounce-counter. | ||
* {{TM|1RB0LC_1LC0RD_1RA1LA_0RA0LA}}, a | * {{TM|1RB0LC_1LC0RD_1RA1LA_0RA0LA}}, a binary bounce-counter with stationary counter digits. | ||
|<div class="text-align: center">[[File:1RB1LC 1LC0RB 1RA0LD 1RA1LA.png|frameless|300x300px]]</div> | |||
|- | |- | ||
|Fractal | |Fractal | ||
| Line 168: | Line 177: | ||
| | | | ||
* {{TM|1RB1RC_0RC0RB_0LD1LA_1LD0LA}}, a typical example. | * {{TM|1RB1RC_0RC0RB_0LD1LA_1LD0LA}}, a typical example. | ||
|<div class="text-align: center">[[File:1RB1RC 0RC0RB 0LD1LA 1LD0LA.png|frameless|300x300px]]</div> | |||
|- | |- | ||
|[[Shift overflow bouncer counter|Tetration counter]] | |[[Shift overflow bouncer counter|Tetration counter]] | ||
| Line 173: | Line 183: | ||
| | | | ||
* {{TM|1RB1LC_0RD0RD_0RC0LA_1LD1RA}}, a typical example. | * {{TM|1RB1LC_0RD0RD_0RC0LA_1LD1RA}}, a typical example. | ||
|<div class="text-align: center">[[File:1RB1LC 0RD0RD 0RC0LA 1LD1RA.png|frameless|300x300px]]</div> | |||
|- | |- | ||
|Cubic | |Cubic bounce-counter | ||
|13 | |13 | ||
| | | | ||
* {{TM|1RB1RA_0LC0RB_0RA0LD_1LC1RD}}, a typical example. Note that these share many of the same properties as [[Dekaheptoid|dekaheptoids]]. | * {{TM|1RB1RA_0LC0RB_0RA0LD_1LC1RD}}, a typical example. Note that these share many of the same properties as [[Dekaheptoid|dekaheptoids]]. | ||
|<div class="text-align: center">[[File:1RB1RA 0LC0RB 0RA0LD 1LC1RD.png|frameless|300x300px]]</div> | |||
|} | |} | ||
==== Chaotic ==== | ==== Chaotic ==== | ||
{| class="wikitable" | {{Table alignment}} | ||
{| class="wikitable col4center" | |||
!Classification | !Classification | ||
!Count | !Count | ||
| Line 192: | Line 205: | ||
* {{TM|1RB0RC_1LC1RA_1RA1LD_0LC0LA}}, a typical irregular bell. | * {{TM|1RB0RC_1LC1RA_1RA1LD_0LC0LA}}, a typical irregular bell. | ||
* {{TM|1RB1LA_0RC0RD_1LD1RC_1LD0LA}}, a typical irregular inverted bell. | * {{TM|1RB1LA_0RC0RD_1LD1RC_1LD0LA}}, a typical irregular inverted bell. | ||
|[[File:1RB0RC 1LC1RA 1RA1LD 0LC0LA.png|frameless]] | |<div class="text-align: center">[[File:1RB0RC 1LC1RA 1RA1LD 0LC0LA.png|frameless|300x300px]]</div> | ||
|- | |- | ||
|[[Spaghetti]] | |[[Spaghetti]] | ||
| Line 199: | Line 212: | ||
* {{TM|1RB0RB_1LC1RC_0RA1LD_1RC0LD}}, a typical spaghetti. | * {{TM|1RB0RB_1LC1RC_0RA1LD_1RC0LD}}, a typical spaghetti. | ||
* {{TM|1RB0RA_1RC0RD_1LD1LC_1RA0LC}}, a spaghetti that seems to converge to a | * {{TM|1RB0RA_1RC0RD_1LD1LC_1RA0LC}}, a spaghetti that seems to converge to a bounce-counter. | ||
* {{TM|1RB1LC_0LA0RD_1LA0LB_1LA1RD}}, a spaghetti whose envelope seems to converge to that of a bouncer. | * {{TM|1RB1LC_0LA0RD_1LA0LB_1LA1RD}}, a spaghetti whose envelope seems to converge to that of a bouncer. | ||
* {{TM|1RB0RC_1LC1LD_1RD1LB_1RA0LB}}, a cellular-automaton-like bouncer. The spaghetti nature of this machine is local. | * {{TM|1RB0RC_1LC1LD_1RD1LB_1RA0LB}}, a cellular-automaton-like bouncer. The spaghetti nature of this machine is local. | ||
* {{TM|1RB1LC_1LA1RD_1RA0LC_1LB0RD}}, a "spaghetti sandwich" -- a spaghetti sandwiched on the left and right by a growing predictable repeating pattern. | * {{TM|1RB1LC_1LA1RD_1RA0LC_1LB0RD}}, a "spaghetti sandwich" -- a spaghetti sandwiched on the left and right by a growing predictable repeating pattern. | ||
|[[File:1RB0RB 1LC1RC 0RA1LD 1RC0LD.png|frameless]] | |<div class="text-align: center">[[File:1RB0RB 1LC1RC 0RA1LD 1RC0LD.png|frameless|300x300px]]</div> | ||
|- | |- | ||
|Chaotic counter | |Chaotic counter | ||
| Line 219: | Line 232: | ||
* {{TM|1RB1LC_0LA0RB_1RD0LC_1LA0RD}} | * {{TM|1RB1LC_0LA0RB_1RD0LC_1LA0RD}} | ||
* {{TM|1RB1LC_1RD0RB_1LA0LC_0LA0RD}} | * {{TM|1RB1LC_1RD0RB_1LA0LC_0LA0RD}} | ||
|[[File:1RB1LC 1RD0RB 1LA0LC 0LA0RD.png|frameless]] | |<div class="text-align: center">[[File:1RB1LC 1RD0RB 1LA0LC 0LA0RD.png|frameless|300x300px]]</div> | ||
|} | |} | ||
Revision as of 19:18, 9 November 2024
A non-halting Turing machine is a Turing machine that does not halt. These include halt-free Turing machines, meaning those without an undefined or halt transition, as well as non-halt-free Turing machines that never enter an undefined or halt transition.
The crux of the Busy Beaver problem, of finding BB(n, k) for a given n and k, is to prove that all non-halting Turing machines with n states and k symbols are, in fact, non-halting.
The zoology of non-halting Turing machines is extremely rich. See Translated cycler, Bouncer, Bell, Counter, Shift overflow counter, Shift overflow bouncer counter for a sample. In this page, we provide a detailed zoology for some low numbers of states and symbols.
Zoology
Machines are enumerated in TNF-1RB, and we exclude halting machines. In particular, a transition is defined if and only if it is reachable; unreachable transitions are undefined. This avoids duplicates.
2 × 2
There are 106 TNF-1RB machines with 2 states and 2 symbols, with the following breakdown:
| Classification | Count | Notable examples |
|---|---|---|
| Translated cycler | 88 | |
| Cycler | 14 | |
| Bouncer | 3 | |
| Counter | 1 |
|
3 × 2
There are 15,064 TNF-1RB machines with 3 states and 2 symbols, with the following breakdown:
| Classification | Count | Notable examples |
|---|---|---|
| Translated cycler | 12,427 | |
| Cycler | 1,969 | |
| Bouncer | 558 |
|
| Counter | 95 | |
| Cubic bell | 10 |
|
| Bell | 5 |
4 × 2
There are 2,744,516 TNF-1RB machines with 4 states and 2 symbols, with the following breakdown. This breakdown is not complete due the chaotic Turing machines. These are the irregular bells, spaghetti, and chaotic counters. These are informal names for chaotic behaviors which escape analysis, and such may well become a translated cycler, or more rarely, a bouncer, after a large number of steps.
Regular (non-chaotic)
| Classification | Count | Notes and Notable examples | Example space-time diagram |
|---|---|---|---|
| Translated cycler | ≥2,253,849 |
|
|
| Cycler | ≥341,617 | ||
| Bouncer | ≈132,000 |
|
|
| Counter | ≈14,700 |
|
|
| Bell | ≈2,350 | ||
| Cubic bell | ≈1,376 | ||
| Bouncer + X | ≈365 |
|
|
| Bounce-counter | ≈330 |
|
|
| Fractal | 20 |
|
|
| Tetration counter | 19 |
|
|
| Cubic bounce-counter | 13 |
|
Chaotic
| Classification | Count | Notes and Notable examples | Example space-time diagram |
|---|---|---|---|
| Irregular bell | 39 | ||
| Spaghetti | 26 | This is an informal description for spaghetti-code Turing machines that seem to have no predictable behavior, instead winding back and forth like a spaghetti. Any of these machines could potentially end up proven as one of the regular classifications. Indeed, many translated cyclers start their life out as spaghetti.
|
|
| Chaotic counter | 10 |
Chaotic counters have slow-growing tapes like counters, but the behavior seems to be chaotic and is as of yet unknown:
|
Records
Translated cycler preperiod
- 3x2: 101 (proven):
1RB1LB_0RC0LA_1LC0LA(bbch) (period = 24) - 4x2: 119,120,230,102 (current champion):
1RB1LC_0LA1RD_0RB0LC_1LA0RD(bbch) (period = 966,716) - 2x4: 293,225,660,896 (current champion):
1RB2LA0RA3LA_1LA1LB3RB1RA(bbch) (period = 483,328)