Translated cycler

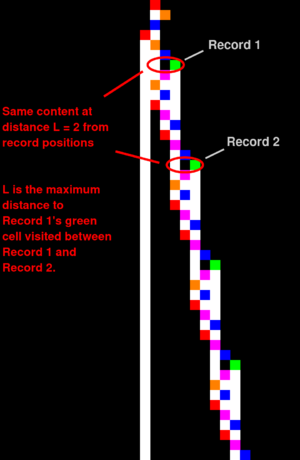
Example "Translated cycler": 45-step space-time diagram of bbchallenge's machine 1RB0RE_0LC1RC_0RD1LA_1LE---_1LB1RC (bbch). The same bounded pattern is being translated to the right forever. The text annotations illustrate the main idea for recognising "Translated Cyclers": find two configurations that break a record (i.e. visit a memory cell that was never visited before) in the same state (here state D) such that the content of the memory tape at distance L from the record positions is the same in both record configurations. Distance L is defined as being the maximum distance to record position 1 that was visited between the configuration of record 1 and record 2.

A translated cycler (also known as a partial recurrent or Lin recurrent TM) is a non-halting Turing machine which eventually exhibits a traveling cyclic behavior. Specifically, a TM has ented a translated cycle once it begins repeating a fixed sequence of transition rules in such a way that it will continue repeating them forever. It is, by far, the most common type of non-halting behavior. For example, 95% of all infinite BB(6) TMs are translated cyclers (which have cycled at least once within the first 1000 steps) and this number is relatively consistent across other BB "domains" (Say BB(5), BB(3,3), etc.).

See Section 3 of bbchallenge's deciders write-up for a formal presentation of translated cyclers.

History

Translated cycling behavior was first described by Shen Lin in his proof of BB(3) where he called it "partial recurrence". He describes an algorithm for detecting it which appears to be the first documented example of a decider. This behavior has been given many names over the years. For example, Nick Drozd calls this Lin recurrence in honor of Shen Lin.

Record breaking

One way to detect translated cycling is by analyzing record breaking configurations. This is the algorithm used by bbchallenge. A Turing machine is a translated cycler if it has two configurations that break a record (i.e. visit a memory cell that was never visited before) in the same state such that the content of the memory tape at distance L from the record positions is the same in both record configurations. Distance L is defined as being the maximum distance to record position 1 that was visited between the configuration of record 1 and record 2.

Here are the properties of the translated cycler shown in the figure:

• L = 2. After the translated cycler reaches record 1, the translated cycler moves at most L = 2 symbols to the left.
• The cycle period is 10 steps. This is the number of steps from record 1 to record 2.
• The cycle offset is 2 symbols to the right. In other words, after each cycle, the TM moves 2 places to the right.
• The cycle start time is 6 steps. This is the position of record 1.

Translated cyclers are close to Cyclers in the sense that they are only repeating a pattern but there is added complexity as they are able to translate the pattern in space at the same time, hence the decider for Cyclers cannot directly apply here.

Infinite shift rule

A translated cycle can be seen as an infinite shift rule. For example, consider the TM 1RB0RE_0LC1RC_0RD1LA_1LE---_1LB1RC (bbch) in the image at the right. It performs the following transition rule:

$${\begin{array}{l}\\10\;{\textrm {D>}}\;00\xrightarrow {10} 00\;10\;{\textrm {D>}}\\\end{array}}$$

which can be repeated to form the shift rule:

$${\begin{array}{l}\\10\;{\textrm {D>}}\;{00}^{n}\xrightarrow {10n} {00}^{n}\;10\;{\textrm {D>}}\\\end{array}}$$

Furthermore, on step 6, this TM is in config

$$0^{\infty }\;1\;10\;{\textrm {D>}}\;0^{\infty }$$

Therefore, we can see that for all $n\geq 0$ we can apply the shift rule and so this TM can never halt.

Notable translated cyclers

Skelet 1 is a translated cycler that has a period of 8,468,569,863 steps, an offset of 107,917 symbols to the right, and a start time of at least $10^{24}$.