Non-halting Turing machine

A non-halting Turing machine is a Turing machine that does not halt. These include halt-free Turing machines, meaning those without an undefined or halt transition, as well as non-halt-free Turing machines that never enter an undefined or halt transition.

The crux of the Busy Beaver problem, of finding BB(n, k) for a given n and k, is to prove that all non-halting Turing machines with n states and k symbols are, in fact, non-halting.

The zoology of non-halting Turing machines is extremely rich. See Translated cycler, Bouncer, Bell, Counter, Fractal, Shift overflow counter, Shift overflow bouncer counter for a sample. In this page, we provide a detailed zoology for some low numbers of states and symbols.

Zoology

Machines are enumerated in TNF-1RB, and we exclude halting machines. In particular, a transition is defined if and only if it is reachable; unreachable transitions are undefined. This avoids duplicates.

For convenience, Turing machines are displayed here in standard text format.

n × 1

There are no TNF-1RB machines with just one symbol, as they cannot have "print 1" in their instructions.

1 × m

There are no non-halting TNF-1RB machines with 1 state and any amount of symbols, as the transition to state B already is undefined and leads to halting.

2 × 2

There are 106 TNF-1RB machines with 2 states and 2 symbols, with the following breakdown:

Classification	Count	Notable examples
Translated cycler	88	1RB0RB_1LB1RA (bbch), unique TM with a record period of 9. 1RB0LB_1LA0RB (bbch), unique TM with a record preperiod of 9.
Cycler	14	1RB0RB_1LB1LA (bbch), one of the 7 TMs with a record period of 4. 1RB1LB_1LA1RA (bbch), unique TM with a record preperiod of 5.
Bouncer	3	1RB1LA_0LA1RB (bbch) 1RB1LA_1LA1RB (bbch) 1RB0LB_1LA0RA (bbch)
Counter	1	1RB1LA_0LA0RB (bbch), a binary counter.

3 × 2

There are 15,064 TNF-1RB machines with 3 states and 2 symbols, with the following breakdown:

Classification	Count	Notable examples
Translated cycler	12,427	1RB0LA_0RC1LA_1LC0RB (bbch), unique TM with a record period of 92. 1RB1LB_0RC0LA_1LC0LA (bbch), unique TM with a record preperiod of 101.
Cycler	1,969	1RB0LB_1LB1LC_0RC1RA (bbch), unique TM with a record period of 18. 1RB1RC_1LC0LB_1RA1LA (bbch), unique TM with a record preperiod of 22.
Bouncer	558	1RB0LC_1RC0RB_1LA1LC (bbch), a bouncer with two distinct shift rules.
Counter	95	1RB1LA_0LA0RC_0LA1RB (bbch), a Fibonacci counter. 1RB1LA_0LA1RC_0LA0RB (bbch), a two-phase binary counter. 1RB1LA_0LA1RC_1LB0RB (bbch), a translating binary counter.
Cubic bell	10	1RB1LA_0LA0RC_0LA1RC (bbch), a typical cubic bell.
Bell	5	1RB0LC_1RC1RA_1LA0RB (bbch), a typical bell. 1RB1LA_0RC0RC_1LC0LA (bbch), a typical inverted bell.

4 × 2

There are 2,744,516 TNF-1RB machines with 4 states and 2 symbols, with the following breakdown. This breakdown is not exact due to the presence of chaotic Turing machines which defy straightforward analysis and may eventually transition into a translated cycler or, more rarely, a bouncer, after a very large number of steps.

Regular (non-chaotic)

Classification	Count	Notes and Notable examples	Example space-time diagram
Translated cycler	≥2,253,849	1RB0LA_0RC1RD_1LD0RB_1LA1RB (bbch), the current period record holder, with a period of 212,081,736. Before phasing into a translated cycle, this machine appears to be a spaghetti (described in a later subsubsection). 1RB1LC_0LA1RD_0RB0LC_1LA0RD (bbch), the current preperiod record holder, with a preperiod of 119,120,230,102. Before phasing into a translated cycle, this machine appears to be a spaghetti. 1RB1RC_1LC0RA_0LB0LD_1LA1LD (bbch) starts out as an irregular bell, but phase transitions into a translated cycler with period 4,222 at step 29,754,825. 1RB0RC_1LB1LD_0RA0LD_1LA1RC (bbch)
Cycler	≥ 341,617	1RB0RB_1LC0RD_1LA1LB_0LC1RD (bbch), likely period record holder, with a period of 120. 1RB1LB_1LC1RD_1LA0RD_0LA0RB (bbch), likely preperiod record holder, with a preperiod of 146.
Bouncer	≈ 132,000	1RB1LA_1LC0RC_0RA1LD_1RC0LD (bbch), the current record holder for longest time to settle into a bouncer, with a start step of 83,158,409. 1RB0RC_0RC0RB_1LC0LD_1LA0RA (bbch), starts out as irregular-side bells before phasing into a bouncer at step 3350. 1RB1LC_0RD0LC_1LB0LA_1LD1RA (bbch), a bouncer with very complex runs. Start step 145,729.
Counter	≈ 14,700	1RB1LC_0LC1RD_1LA1LB_0LC0RD (bbch), a ternary counter. 1RB1LC_0LA1RB_1LD0RB_1LA1RA (bbch), a quaternary counter. 1RB0LB_1RC0LD_1LB1RA_0RB1LD (bbch), a quinary counter. 1RB1LC_0LD1RB_1LD0RD_1LA0RB (bbch), a senary counter. 1RB1LC_0LD0RB_1RD1LA_1RA0LC (bbch), a 3/2-counter. 1RB0RA_1LC1RA_1LD0LC_1LA1LD (bbch), a binary bi-counter. 1RB1LC_1RC1RB_1RD0LC_1LA0RD (bbch), a binary-ternary bi-counter. 1RB1LA_0LA0RC_0LA0RD_0LA1RC (bbch), a counter encoding a recurrence with characteristic polynomial $x^3-x^2-2x+1$. 1RB1LA_0LA0RC_0LA1RD_0LA0RB (bbch), a counter encoding a recurrence with characteristic polynomial $x^3-x^2-2$. 1RB1LC_1LD1RA_0RA0LC_0RB0LD (bbch), a counter encoding a recurrence that grows like $n\cdot 2^n$. 1RB0RC_0LC0RA_1LA0LD_1RA1LD (bbch), a tri-phasic binary counter. 1RB1LC_0RD0RB_1LA0LA_1LD0LA (bbch), an example of a superexponential counter.
Bell	≈ 2,350	1RB1LA_0RC0LD_1LC0LA_1RC0RD (bbch), a typical inverted bell. 1RB1LB_1LC0RA_1RD0LB_1LA1RC (bbch), alternates between bell and half-bell. 1RB0LC_1RC1RB_1LA1LD_0RA0RB (bbch), a grow-and-shrink bell. 1RB0RC_1LC0RA_1RA1LD_0LC0LA (bbch), starts out as an irregular bell before phasing into a bell.
Cubic bell	≈ 1,376	1RB1RC_1LC0RC_0RA1LD_0LC0LB (bbch), a cubic inverted bell. 1RB0RC_0LD0RA_0LA1RC_1LA1LD (bbch), a cubic grow-and-shrink bell.
Bouncer + X	≈ 365	1RB1LA_1RC0RB_0LC1LD_0LD1RA (bbch), a bouncer + binary counter. 1RB0LA_0RC1LA_1RD0RA_0LB1RB (bbch), a bouncer + bell. 1RB1LC_0RC1RD_1LA0LA_1RC0RB (bbch), a bouncer + cellular automaton. This could be universal. 1RB1LC_0RC1RD_1LA0LA_0LA0RB (bbch), a bouncer + cellular automaton with a fractal nature. 1RB1LB_0LC0RD_0RA1LC_1RA1RD (bbch), a bouncer + cubic bell, leading to quartic tape growth on the left. 1RB0LC_1LA1RD_1RA1LD_0LA0RB (bbch), a bouncer + unclassified. (If you can classify it, let me know in the talk page!)
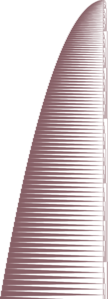
Bounce-counter	≈ 330	1RB1LC_1LC0RB_1RA0LD_1RA1LA (bbch), a typical binary bounce-counter. 1RB1LB_1RC1RD_0LA0RC_1LD0LB (bbch), a typical quaternary bounce-counter. 1RB1RA_0RC0LC_1LA0LD_0RA1LC (bbch), a ternary bounce-counter, which is more rare. 1RB0LA_0RC1LA_0RD1RB_1LD1LA (bbch), a hybrid quaternary-octal bounce-counter. 1RB0LC_1RD0RB_1LA1RC_1LC1RB (bbch), a 3/2-bounce-counter. 1RB0LC_1LC0RD_1RA1LA_0RA0LA (bbch), a binary bounce-counter with stationary counter digits.
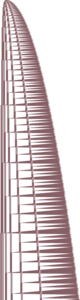
Fractal	20	1RB1RC_0RC0RB_0LD1LA_1LD0LA (bbch), a typical example.
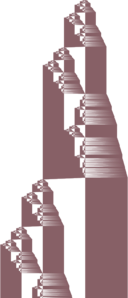
Tetration counter	19	1RB1LC_0RD0RD_0RC0LA_1LD1RA (bbch), a typical example.
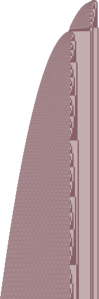
Cubic bounce-counter	13	1RB1RA_0LC0RB_0RA0LD_1LC1RD (bbch), a typical example. Note that these share many of the same properties as dekaheptoids.

Chaotic

Classification	Count	Notes and Notable examples	Example space-time diagram
Irregular bell	39	1RB0RC_1LC1RA_1RA1LD_0LC0LA (bbch), a typical irregular bell. 1RB1LA_0RC0RD_1LD1RC_1LD0LA (bbch), a typical irregular inverted bell.
Spaghetti	26	This is an informal description for spaghetti-code Turing machines that seem to have no predictable behavior, instead winding back and forth like a spaghetti. Any of these machines could potentially end up proven as one of the regular classifications. Indeed, many translated cyclers start their life out as spaghetti. 1RB0RB_1LC1RC_0RA1LD_1RC0LD (bbch), a typical spaghetti. 1RB0RA_1RC0RD_1LD1LC_1RA0LC (bbch), a spaghetti that seems to converge to a bounce-counter. 1RB1LC_0LA0RD_1LA0LB_1LA1RD (bbch), a spaghetti whose envelope seems to converge to that of a bouncer. 1RB0RC_1LC1LD_1RD1LB_1RA0LB (bbch), a cellular-automaton-like bouncer. The spaghetti nature of this machine is local. 1RB1LC_1LA1RD_1RA0LC_1LB0RD (bbch), a "spaghetti sandwich" -- a spaghetti sandwiched on the left and right by a growing predictable repeating pattern.
Chaotic counter	10	Chaotic counters have slow-growing tapes like counters, but the behavior seems to be chaotic and is as of yet unknown: 1RB0RC_0LD1RC_1LD0RB_0LA1LA (bbch) 1RB1RA_0LC0LD_1LD0RB_0RA1LC (bbch) 1RB0RC_1LA1RC_0LD0RB_0LA1LD (bbch) 1RB0RB_1LC1RA_1LD0LC_0RA0LD (bbch) 1RB1LA_0RC1RC_0LD0RB_0LA1LD (bbch) 1RB1LC_0LC0RD_0LA1LA_0RB1RD (bbch) 1RB0RB_0LC1RA_1LD1LC_0RA0LD (bbch) 1RB1LC_1LD0RB_1RA0LC_0RA0LD (bbch) 1RB1LC_0LA0RB_1RD0LC_1LA0RD (bbch) 1RB1LC_1RD0RB_1LA0LC_0LA0RD (bbch)

Records

Translated cycler preperiod

BBS(n,m) = maximum translated cycler preperiod among n-state, m-symbol TMs.

BBS(1,m) = 0: 0RA--- (bbch) and 1RA--- (bbch), note that any transitions other than A0 are unreachable.

Domain	Preperiod	Champions	Period
BBS(2,2)	≥ 9	1RB0LB_1LA0RB (bbch)	3
BBS(3,2)	= 101	1RB1LB_0RC0LA_1LC0LA (bbch)	24
BBS(4,2)	≥ 119,120,230,102	1RB1LC_0LA1RD_0RB0LC_1LA0RD (bbch)	966,716
BBS(5,2)	> 1014,006	1RB1LE_0LC0LB_0LD1LC_1RD1RA_0RC0LA (bbch)	1
BBS(2,3)	≥ 165	1RB0LA---_1LB2LA0RB (bbch)	55
BBS(3,3)	> 10 ↑↑ 6	1RB0LB2LA_1LA0RC0LB_2RC2RB0LC (bbch)	1
BBS(4,3)	> $10{\uparrow }^{4}4$	1RB1RD1LC_2LB1RB1LC_1LB1LA1LD_0RB2RA2RD (bbch)	1
BBS(2,4)	≥ 205,770,076,433,044,242,247,860	1RB2LA1RA1LB_0LB2RB3RB1LA (bbch)	1

Translated cycler period

BBP(n,m) = maximum translated cycler period among n-state, m-symbol TMs.

BBP(1,m) = 1: 0RA--- (bbch) and 1RA--- (bbch), note that any transitions other than A0 are unreachable.

Domain	Period	Champions	Preperiod
BBP(2,2)	≥ 9	1RB0RB_1LB1RA (bbch)	0
BBP(3,2)	= 92	1RB0LA_0RC1LA_1LC0RB (bbch)	0
BBP(4,2)	≥ 212,081,736	1RB0LA_0RC1RD_1LD0RB_1LA1RB (bbch)	5,248,647,886
BBP(3,3)	≥ 1,195	1RB2RC1LC_0RC0RB1LA_2LA2RC1LB (bbch)	15
BBP(2,4)	≥ 33,209,131	1RB0RA3LB1RB_2LA0LB1RA2RB (bbch)	63,141,841