Cycler: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
(Mentioned BBS and BBP) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:1RB0LB 1LB1LC 0RC1RA.png|alt=1RB0LB_1LB1LC_0RC1RA|thumb|upright=1.5|The record 3-state 2-symbol cycler {{TM|1RB0LB_1LB1LC_0RC1RA}}, which has period 18 and preperiod 4.]] | [[File:1RB0LB 1LB1LC 0RC1RA.png|alt=1RB0LB_1LB1LC_0RC1RA|thumb|upright=1.5|The record 3-state 2-symbol cycler {{TM|1RB0LB_1LB1LC_0RC1RA}}, which has period 18 and preperiod 4.]]{{Stub}} | ||
A '''cycler''' is a Turing machine that eventually enters a repeating cycle. Such a Turing machine runs forever | A '''cycler''' is a Turing machine that eventually enters a repeating cycle. Such a Turing machine runs forever and thus is a [[non-halting Turing machine]]. A cycler may be seen as a special case of a [[translated cycler]] which has offset zero. | ||
The rule for identifying cyclers is simple: | The rule for identifying cyclers is simple: | ||
'''û''' → '''û''' | '''û''' → '''û''' | ||
where '''û''' is any headed tape segment. | where '''û''' is any headed tape segment. | ||
==Related Functions== | |||
* Busy Preperiodic Beaver ([[BBS]](n,m)): The longest possible preperiod of a cycler or translated cycler with n states and m symbols. | |||
* Busy Periodic Beaver ([[BBP]](n,m)): The longest possible period of a cycler or translated cycler with n states and m symbols. | |||
== See also == | == See also == | ||
* [[Translated cycler]] | * [[Translated cycler]] | ||
* [https://github.com/bbchallenge/bbchallenge-proofs/blob/build-latex-pdf/deciders/correctness-deciders.pdf Section 2] of bbchallenge's deciders write-up. | |||
[[Category:Zoology]] | [[Category:Zoology]] | ||
Latest revision as of 11:01, 17 August 2025
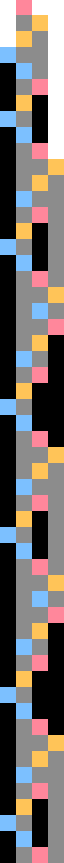
1RB0LB_1LB1LC_0RC1RA (bbch), which has period 18 and preperiod 4.A cycler is a Turing machine that eventually enters a repeating cycle. Such a Turing machine runs forever and thus is a non-halting Turing machine. A cycler may be seen as a special case of a translated cycler which has offset zero.
The rule for identifying cyclers is simple:
û → û
where û is any headed tape segment.
Related Functions
- Busy Preperiodic Beaver (BBS(n,m)): The longest possible preperiod of a cycler or translated cycler with n states and m symbols.
- Busy Periodic Beaver (BBP(n,m)): The longest possible period of a cycler or translated cycler with n states and m symbols.
See also
- Translated cycler
- Section 2 of bbchallenge's deciders write-up.