Bouncer: Difference between revisions
Jump to navigation
Jump to search
m →Example |
Used Template:Stub |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:1RB0LB 1LA0RA.png|alt=1RB0LB_1LA0RA|thumb|A close-up of the bouncer {{TM|1RB0LB_1LA0RA}} with 2 states, the smallest number of states for which a bouncer can appear.]] | [[File:1RB0LB 1LA0RA.png|alt=1RB0LB_1LA0RA|thumb|A close-up of the bouncer {{TM|1RB0LB_1LA0RA}} with 2 states, the smallest number of states for which a bouncer can appear.]]{{Stub}} | ||
A '''bouncer''' is a Turing machine whose tape head, roughly speaking, alternates back and forth between the two edges of the tape in a linear fashion, growing the tape along one or both edges with each iteration | A '''bouncer''' is a [[non-halting Turing machine]] whose tape head, roughly speaking, alternates back and forth between the two edges of the tape in a linear fashion, growing the tape along one or both edges with each iteration. | ||
== Example == | == Example == | ||
| Line 6: | Line 6: | ||
=== Analysis === | === Analysis === | ||
'''[[Transcript]]''': (A0 (B0 A1)<sup>2n+1</sup> B0 (A0 B1)<sup>2n+2</sup>)<sup>n≥0</sup>. | |||
The derivation of this transcript is as follows. | |||
'''Shift rules:''' | '''Shift rules:''' | ||
| Line 15: | Line 19: | ||
* '''B'''<sub>n</sub> := A0 (B0 A1)<sup>2n+1</sup> B0 (A0 B1)<sup>2n+2</sup>: <code>A 00(10<sup>2n</sup>)>00 →[8n+8] A (10<sup>2(n+1)</sup>)></code> | * '''B'''<sub>n</sub> := A0 (B0 A1)<sup>2n+1</sup> B0 (A0 B1)<sup>2n+2</sup>: <code>A 00(10<sup>2n</sup>)>00 →[8n+8] A (10<sup>2(n+1)</sup>)></code> | ||
In particular, we have | In particular, we have<blockquote>'''B'''<sub>n</sub>: <code>A 0<sup>∞</sup>(10<sup>2n</sup>)>0<sup>∞</sup> →[8n+8] 0<sup>∞</sup>(10<sup>2(n+1)</sup>)>0<sup>∞</sup></code>,</blockquote>which by induction proves that the transcript of <code>1RB0LB_1LA0RA</code> on the all-zeros tape is ('''B'''<sub>n</sub>)<sup>n≥0</sup>. Moreover, we have shown that there are 8''n'' + 8 steps between the ''n''<sup>th</sup> and the (''n''+1)<sup>st</sup> bounce. | ||
'''B'''<sub>n</sub>: <code>A 0<sup>∞</sup>(10<sup>2n</sup>)>0<sup>∞</sup> →[8n+8] 0<sup>∞</sup>(10<sup>2(n+1)</sup>)>0<sup>∞</sup></code>, | |||
which by induction proves that the transcript of <code>1RB0LB_1LA0RA</code> on the all-zeros tape is ('''B'''<sub>n</sub>)<sup>n≥0</sup> | |||
== See also == | == See also == | ||
| Line 26: | Line 26: | ||
[[Category:Zoology]] | [[Category:Zoology]] | ||
Latest revision as of 22:29, 10 August 2025
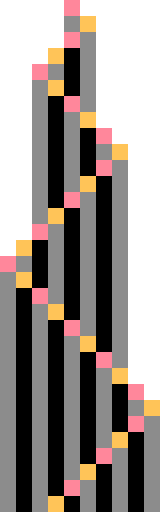
1RB0LB_1LA0RA (bbch) with 2 states, the smallest number of states for which a bouncer can appear.A bouncer is a non-halting Turing machine whose tape head, roughly speaking, alternates back and forth between the two edges of the tape in a linear fashion, growing the tape along one or both edges with each iteration.
Example
1RB0LB_1LA0RA (bbch) is an example of a bouncer, and its spacetime diagram is shown in the picture on the right.
Analysis
Transcript: (A0 (B0 A1)2n+1 B0 (A0 B1)2n+2)n≥0.
The derivation of this transcript is as follows.
Shift rules:
- B0 A1:
B 10< →[2] B <01, - A0 B1:
A >10 →[2] A 01>.
Bounce rule:
- Bn := A0 (B0 A1)2n+1 B0 (A0 B1)2n+2:
A 00(102n)>00 →[8n+8] A (102(n+1))>
In particular, we have
Bn:
A 0∞(102n)>0∞ →[8n+8] 0∞(102(n+1))>0∞,
which by induction proves that the transcript of 1RB0LB_1LA0RA on the all-zeros tape is (Bn)n≥0. Moreover, we have shown that there are 8n + 8 steps between the nth and the (n+1)st bounce.
See also
- Section 7 of bbchallenge's deciders write-up.