Bell: Difference between revisions
Add correct machine and bbch link →Examples |
Used Template:Stub |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{Stub}} | |||
A '''bell''' is a [[non-halting Turing machine]] whose behavior can be described as a sequence of [[bouncer]]s of increasing size. There are two main variants of bells, depending on whether the bouncers participate in tape growth or not. A bell whose bouncers grow the tape on each bounce is called an '''exponential bell''' or simply '''bell''' for short, while a bell whose bouncers do not grow the tape on each bounce is called a '''cubic bell'''. | A '''bell''' is a [[non-halting Turing machine]] whose behavior can be described as a sequence of [[bouncer]]s of increasing size. There are two main variants of bells, depending on whether the bouncers participate in tape growth or not. A bell whose bouncers grow the tape on each bounce is called an '''exponential bell''' or simply '''bell''' for short, while a bell whose bouncers do not grow the tape on each bounce is called a '''cubic bell'''. | ||
| Line 11: | Line 12: | ||
==== Analysis ==== | ==== Analysis ==== | ||
'''Transcript''': (A0 B0 ((C1 B0)<sup>2k</sup> (C0 A1)<sup>2k+1</sup>)<sup>(k = 0 .. n-1)</sup> (C0 B1)<sup>2n</sup> (C0 A1)<sup>2n</sup> C0 (A0 B1)<sup>2n+1</sup>)<sup>n=''a''<sub>0</sub>, ''a''<sub>1</sub>, ...</sup>, | '''[[Transcript]]''': (A0 B0 ((C1 B0)<sup>2k</sup> (C0 A1)<sup>2k+1</sup>)<sup>(k = 0 .. n-1)</sup> (C0 B1)<sup>2n</sup> (C0 A1)<sup>2n</sup> C0 (A0 B1)<sup>2n+1</sup>)<sup>n=''a''<sub>0</sub>, ''a''<sub>1</sub>, ...</sup>, | ||
where <math>a_0=1</math> and <math>a_k=2a_{k-1}+3\text{ for }k\geq 1.</math> | where <math>a_0=1</math> and <math>a_k=2a_{k-1}+3\text{ for }k\geq 1.</math> | ||
| Line 23: | Line 24: | ||
[[Category: Zoology]] | [[Category: Zoology]] | ||
Latest revision as of 22:28, 10 August 2025
A bell is a non-halting Turing machine whose behavior can be described as a sequence of bouncers of increasing size. There are two main variants of bells, depending on whether the bouncers participate in tape growth or not. A bell whose bouncers grow the tape on each bounce is called an exponential bell or simply bell for short, while a bell whose bouncers do not grow the tape on each bounce is called a cubic bell.
Sometimes a Turing machine displays bell characteristics for some number of steps before phase transitioning to another behavior, such as halting. A famous example is the 5-state busy beaver winner. These may also be called bells, or more precisely, transient bells, to indicate that they only show bell-like features up to a certain point.
Examples

1RB0LC_1RC1RA_1LA0RB (bbch).Exponential bell
1RB0LC_1RC1RA_1LA0RB (bbch) is an example of an exponential bell with 3 states and 2 symbols.
Analysis
Transcript: (A0 B0 ((C1 B0)2k (C0 A1)2k+1)(k = 0 .. n-1) (C0 B1)2n (C0 A1)2n C0 (A0 B1)2n+1)n=a0, a1, ...,
where and

1RB0LC_1LA1RB_0RA1LC (bbch).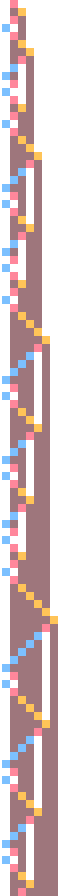
1RB0LC_1LA1RB_0RA1LC (bbch).Cubic bell
1RB0LC_1LA1RB_0RA1LC (bbch) is an example of a cubic bell with 3 states and 2 symbols.
Analysis
Transcript: ((A0 B1k B0 A1 C1k C0 A1 C0)(k = n, n-1, .. 1) A0 B0 A1 C0)(n ≥ 0).