Non-halting Turing machine: Difference between revisions
m (→Zoology) |
(→Records: Name BBS function) |
||
| (9 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
The crux of the [[Busy Beaver function|Busy Beaver]] problem, of finding BB(''n'', ''k'') for a given ''n'' and ''k'', is to prove that all non-halting Turing machines with ''n'' states and ''k'' symbols are, in fact, non-halting. | The crux of the [[Busy Beaver function|Busy Beaver]] problem, of finding BB(''n'', ''k'') for a given ''n'' and ''k'', is to prove that all non-halting Turing machines with ''n'' states and ''k'' symbols are, in fact, non-halting. | ||
The zoology of non-halting Turing machines is extremely rich. See [[Translated cycler]], [[Bouncer]], [[Bell]], [[Counter]], [[Shift overflow counter]], [[Shift overflow bouncer counter]] for a sample. In this page, we provide a detailed zoology for some low numbers of states and symbols. | The zoology of non-halting Turing machines is extremely rich. See [[Translated cycler]], [[Bouncer]], [[Bell]], [[Counter]], [[Fractal]], [[Shift overflow counter]], [[Shift overflow bouncer counter]] for a sample. In this page, we provide a detailed zoology for some low numbers of states and symbols. | ||
== Zoology == | == Zoology == | ||
Machines are enumerated in [[TNF-1RB]], and we exclude halting machines. In particular, a transition is defined if and only if it is reachable; unreachable transitions are undefined. This avoids duplicates. | Machines are enumerated in [[TNF-1RB]], and we exclude halting machines. In particular, a transition is defined if and only if it is reachable; unreachable transitions are undefined. This avoids duplicates. | ||
For convenience, Turing machines are displayed here in [[ | For convenience, Turing machines are displayed here in [[Turing machine#Standard text format|standard text format]]. | ||
=== 2 × 2 === | === 2 × 2 === | ||
| Line 74: | Line 74: | ||
* {{TM|1RB1LA_0LA1RC_1LB0RB}}, a translating binary counter. | * {{TM|1RB1LA_0LA1RC_1LB0RB}}, a translating binary counter. | ||
|- | |- | ||
|[[Cubic bell]] | |[[Bell|Cubic bell]] | ||
|10 | |10 | ||
| | | | ||
| Line 87: | Line 87: | ||
=== 4 × 2 === | === 4 × 2 === | ||
There are 2,744,516 TNF-1RB machines with 4 states and 2 symbols, with the following breakdown. This breakdown is not | There are 2,744,516 TNF-1RB machines with 4 states and 2 symbols, with the following breakdown. This breakdown is not exact due to the presence of chaotic Turing machines which defy straightforward analysis and may eventually transition into a translated cycler or, more rarely, a bouncer, after a very large number of steps. | ||
==== Regular (non-chaotic) ==== | ==== Regular (non-chaotic) ==== | ||
| Line 99: | Line 99: | ||
|≥2,253,849 | |≥2,253,849 | ||
| | | | ||
* {{TM|1RB0LA_0RC1RD_1LD0RB_1LA1RB}}, the current period record holder, with a period of 212,081,736. Before phasing into a translated cycle, this machine appears to be a | * {{TM|1RB0LA_0RC1RD_1LD0RB_1LA1RB}}, the current period record holder, with a period of 212,081,736. Before phasing into a translated cycle, this machine appears to be a spaghetti (described in a later subsubsection). | ||
* {{TM|1RB1LC_0LA1RD_0RB0LC_1LA0RD}}, the current preperiod record holder, with a preperiod of 119,120,230,102. Before phasing into a translated cycle, this machine appears to be a | * {{TM|1RB1LC_0LA1RD_0RB0LC_1LA0RD}}, the current preperiod record holder, with a preperiod of 119,120,230,102. Before phasing into a translated cycle, this machine appears to be a spaghetti. | ||
* {{TM|1RB1RC_1LC0RA_0LB0LD_1LA1LD}} starts out as an irregular bell, but phase transitions into a translated cycler with period 4,222 at step 29,754,825. | * {{TM|1RB1RC_1LC0RA_0LB0LD_1LA1LD}} starts out as an irregular bell, but phase transitions into a translated cycler with period 4,222 at step 29,754,825. | ||
| | * {{TM|1RB0RC_1LB1LD_0RA0LD_1LA1RC}} | ||
|[[File:1RB0RC 1LB1LD 0RA0LD 1LA1RC.png|frameless]] | |||
|- | |- | ||
|[[Cycler]] | |[[Cycler]] | ||
| | |≥ 341,617 | ||
| | | | ||
* {{TM|1RB0RB_1LC0RD_1LA1LB_0LC1RD}}, likely period record holder, with a period of 120. | * {{TM|1RB0RB_1LC0RD_1LA1LB_0LC1RD}}, likely period record holder, with a period of 120. | ||
| Line 112: | Line 113: | ||
|- | |- | ||
|[[Bouncer]] | |[[Bouncer]] | ||
| | |≈ 132,000 | ||
| | | | ||
* {{TM|1RB1LA_1LC0RC_0RA1LD_1RC0LD}}, the current record holder for longest time to settle into a bouncer, with a start step of 83,158,409. | * {{TM|1RB1LA_1LC0RC_0RA1LD_1RC0LD}}, the current record holder for longest time to settle into a bouncer, with a start step of 83,158,409. | ||
| Line 120: | Line 121: | ||
|- | |- | ||
|[[Counter]] | |[[Counter]] | ||
| | |≈ 14,700 | ||
| | | | ||
* {{TM|1RB1LC_0LC1RD_1LA1LB_0LC0RD}}, a ternary counter. | * {{TM|1RB1LC_0LC1RD_1LA1LB_0LC0RD}}, a ternary counter. | ||
| Line 138: | Line 139: | ||
|- | |- | ||
|[[Bell]] | |[[Bell]] | ||
| | |≈ 2,350 | ||
| | | | ||
* {{TM|1RB1LA_0RC0LD_1LC0LA_1RC0RD}}, a typical inverted bell. | * {{TM|1RB1LA_0RC0LD_1LC0LA_1RC0RD}}, a typical inverted bell. | ||
| Line 146: | Line 147: | ||
| | | | ||
|- | |- | ||
|[[Cubic bell]] | |[[Bell|Cubic bell]] | ||
| | |≈ 1,376 | ||
| | | | ||
* {{TM|1RB1RC_1LC0RC_0RA1LD_0LC0LB}}, a cubic inverted bell. | * {{TM|1RB1RC_1LC0RC_0RA1LD_0LC0LB}}, a cubic inverted bell. | ||
| Line 154: | Line 155: | ||
|- | |- | ||
|Bouncer + X | |Bouncer + X | ||
| | |≈ 365 | ||
| | | | ||
* {{TM|1RB1LA_1RC0RB_0LC1LD_0LD1RA}}, a bouncer + binary counter. | * {{TM|1RB1LA_1RC0RB_0LC1LD_0LD1RA}}, a bouncer + binary counter. | ||
| Line 162: | Line 163: | ||
* {{TM|1RB1LB_0LC0RD_0RA1LC_1RA1RD}}, a bouncer + cubic bell, leading to quartic tape growth on the left. | * {{TM|1RB1LB_0LC0RD_0RA1LC_1RA1RD}}, a bouncer + cubic bell, leading to quartic tape growth on the left. | ||
* {{TM|1RB0LC_1LA1RD_1RA1LD_0LA0RB}}, a bouncer + unclassified. (If you can classify it, let me know in the talk page!) | * {{TM|1RB0LC_1LA1RD_1RA1LD_0LA0RB}}, a bouncer + unclassified. (If you can classify it, let me know in the talk page!) | ||
| | |style="text-align: center"|[[File:1RB0LB_1LC1RA_1RD0LC_0LA0RB.png|alt=Bouncer + counter|frameless|300x300px|Bouncer + counter.]] | ||
[[File:1RB1LC 0RC1RD 1LA0LA 1RC0RB.png|alt=Bouncer + cellular automaton|frameless|Bouncer + cellular automaton.]] | |||
|- | |- | ||
|Bounce-counter | |Bounce-counter | ||
| | |≈ 330 | ||
| | | | ||
* {{TM|1RB1LC_1LC0RB_1RA0LD_1RA1LA}}, a typical binary bounce-counter. | * {{TM|1RB1LC_1LC0RB_1RA0LD_1RA1LA}}, a typical binary bounce-counter. | ||
| Line 174: | Line 175: | ||
* {{TM|1RB0LC_1RD0RB_1LA1RC_1LC1RB}}, a 3/2-bounce-counter. | * {{TM|1RB0LC_1RD0RB_1LA1RC_1LC1RB}}, a 3/2-bounce-counter. | ||
* {{TM|1RB0LC_1LC0RD_1RA1LA_0RA0LA}}, a binary bounce-counter with stationary counter digits. | * {{TM|1RB0LC_1LC0RD_1RA1LA_0RA0LA}}, a binary bounce-counter with stationary counter digits. | ||
| | |style="text-align: center"|[[File:1RB1LC 1LC0RB 1RA0LD 1RA1LA.png|frameless|300x300px]] | ||
|- | |- | ||
|Fractal | |[[Fractal]] | ||
|20 | |20 | ||
| | | | ||
* {{TM|1RB1RC_0RC0RB_0LD1LA_1LD0LA}}, a typical example. | * {{TM|1RB1RC_0RC0RB_0LD1LA_1LD0LA}}, a typical example. | ||
| | |style="text-align: center"|[[File:1RB1RC 0RC0RB 0LD1LA 1LD0LA.png|frameless|300x300px]] | ||
|- | |- | ||
|[[Shift overflow bouncer counter|Tetration counter]] | |[[Shift overflow bouncer counter|Tetration counter]] | ||
| Line 186: | Line 187: | ||
| | | | ||
* {{TM|1RB1LC_0RD0RD_0RC0LA_1LD1RA}}, a typical example. | * {{TM|1RB1LC_0RD0RD_0RC0LA_1LD1RA}}, a typical example. | ||
| | |style="text-align: center"|[[File:1RB1LC 0RD0RD 0RC0LA 1LD1RA.png|frameless|300x300px]] | ||
|- | |- | ||
|Cubic bounce-counter | |Cubic bounce-counter | ||
| Line 192: | Line 193: | ||
| | | | ||
* {{TM|1RB1RA_0LC0RB_0RA0LD_1LC1RD}}, a typical example. Note that these share many of the same properties as [[Dekaheptoid|dekaheptoids]]. | * {{TM|1RB1RA_0LC0RB_0RA0LD_1LC1RD}}, a typical example. Note that these share many of the same properties as [[Dekaheptoid|dekaheptoids]]. | ||
| | |style="text-align: center"|[[File:1RB1RA 0LC0RB 0RA0LD 1LC1RD.png|frameless|300x300px]] | ||
|} | |} | ||
| Line 207: | Line 208: | ||
* {{TM|1RB0RC_1LC1RA_1RA1LD_0LC0LA}}, a typical irregular bell. | * {{TM|1RB0RC_1LC1RA_1RA1LD_0LC0LA}}, a typical irregular bell. | ||
* {{TM|1RB1LA_0RC0RD_1LD1RC_1LD0LA}}, a typical irregular inverted bell. | * {{TM|1RB1LA_0RC0RD_1LD1RC_1LD0LA}}, a typical irregular inverted bell. | ||
| | |style="text-align: center"|[[File:1RB0RC 1LC1RA 1RA1LD 0LC0LA.png|frameless|300x300px]] | ||
|- | |- | ||
| | |Spaghetti | ||
|26 | |26 | ||
|This is an informal description for spaghetti-code Turing machines that seem to have no predictable behavior, instead winding back and forth like a spaghetti. Any of these machines could potentially end up proven as one of the regular classifications. Indeed, many translated cyclers start their life out as spaghetti. | |This is an informal description for spaghetti-code Turing machines that seem to have no predictable behavior, instead winding back and forth like a spaghetti. Any of these machines could potentially end up proven as one of the regular classifications. Indeed, many translated cyclers start their life out as spaghetti. | ||
| Line 218: | Line 219: | ||
* {{TM|1RB0RC_1LC1LD_1RD1LB_1RA0LB}}, a cellular-automaton-like bouncer. The spaghetti nature of this machine is local. | * {{TM|1RB0RC_1LC1LD_1RD1LB_1RA0LB}}, a cellular-automaton-like bouncer. The spaghetti nature of this machine is local. | ||
* {{TM|1RB1LC_1LA1RD_1RA0LC_1LB0RD}}, a "spaghetti sandwich" -- a spaghetti sandwiched on the left and right by a growing predictable repeating pattern. | * {{TM|1RB1LC_1LA1RD_1RA0LC_1LB0RD}}, a "spaghetti sandwich" -- a spaghetti sandwiched on the left and right by a growing predictable repeating pattern. | ||
| | |style="text-align: center"|[[File:1RB0RB 1LC1RC 0RA1LD 1RC0LD.png|frameless|300x300px]] | ||
|- | |- | ||
|Chaotic counter | |Chaotic counter | ||
| Line 234: | Line 235: | ||
* {{TM|1RB1LC_0LA0RB_1RD0LC_1LA0RD}} | * {{TM|1RB1LC_0LA0RB_1RD0LC_1LA0RD}} | ||
* {{TM|1RB1LC_1RD0RB_1LA0LC_0LA0RD}} | * {{TM|1RB1LC_1RD0RB_1LA0LC_0LA0RD}} | ||
| | |style="text-align: center"|[[File:1RB1LC 1RD0RB 1LA0LC 0LA0RD.png|frameless|300x300px]] | ||
|} | |} | ||
| Line 240: | Line 241: | ||
=== Translated cycler preperiod === | === Translated cycler preperiod === | ||
* | BBS(n,m) = maximum translated cycler preperiod among n-state, m-symbol TMs. | ||
* | * BBS(3,2) = 101 (proven): {{TM|1RB1LB_0RC0LA_1LC0LA}} (period = 24) | ||
* | * BBS(4,2) ≥ 119,120,230,102 (current champion): {{TM|1RB1LC_0LA1RD_0RB0LC_1LA0RD}} (period = 966,716) | ||
* BBS(2,4) ≥ 293,225,660,896 (current champion): {{TM|1RB2LA0RA3LA_1LA1LB3RB1RA}} (period = 483,328) | |||
=== Translated cycler period === | === Translated cycler period === | ||
* | BBP(n,m) = maximum translated cycler period among n-state, m-symbol TMs. | ||
* | * BBP(3,2) = 92 (proven): {{TM|1RB0LA_0RC1LA_1LC0RB}} (preperiod = 0) | ||
* | * BBP(4,2) ≥ 212,081,736 (current champion): {{TM|1RB0LA_0RC1RD_1LD0RB_1LA1RB}} (preperiod = 5,248,647,886) | ||
* BBP(2,4) ≥ 33,209,131 (current champion): {{TM|1RB0RA3LB1RB_2LA0LB1RA2RB}} (preperiod = 63,141,841) | |||
Latest revision as of 01:39, 30 July 2025
A non-halting Turing machine is a Turing machine that does not halt. These include halt-free Turing machines, meaning those without an undefined or halt transition, as well as non-halt-free Turing machines that never enter an undefined or halt transition.
The crux of the Busy Beaver problem, of finding BB(n, k) for a given n and k, is to prove that all non-halting Turing machines with n states and k symbols are, in fact, non-halting.
The zoology of non-halting Turing machines is extremely rich. See Translated cycler, Bouncer, Bell, Counter, Fractal, Shift overflow counter, Shift overflow bouncer counter for a sample. In this page, we provide a detailed zoology for some low numbers of states and symbols.
Zoology
Machines are enumerated in TNF-1RB, and we exclude halting machines. In particular, a transition is defined if and only if it is reachable; unreachable transitions are undefined. This avoids duplicates.
For convenience, Turing machines are displayed here in standard text format.
2 × 2
There are 106 TNF-1RB machines with 2 states and 2 symbols, with the following breakdown:
| Classification | Count | Notable examples |
|---|---|---|
| Translated cycler | 88 | |
| Cycler | 14 | |
| Bouncer | 3 | |
| Counter | 1 |
|
3 × 2
There are 15,064 TNF-1RB machines with 3 states and 2 symbols, with the following breakdown:
| Classification | Count | Notable examples |
|---|---|---|
| Translated cycler | 12,427 | |
| Cycler | 1,969 | |
| Bouncer | 558 |
|
| Counter | 95 | |
| Cubic bell | 10 |
|
| Bell | 5 |
4 × 2
There are 2,744,516 TNF-1RB machines with 4 states and 2 symbols, with the following breakdown. This breakdown is not exact due to the presence of chaotic Turing machines which defy straightforward analysis and may eventually transition into a translated cycler or, more rarely, a bouncer, after a very large number of steps.
Regular (non-chaotic)
| Classification | Count | Notes and Notable examples | Example space-time diagram |
|---|---|---|---|
| Translated cycler | ≥2,253,849 |
|

|
| Cycler | ≥ 341,617 | ||
| Bouncer | ≈ 132,000 |
|
|
| Counter | ≈ 14,700 |
|
|
| Bell | ≈ 2,350 | ||
| Cubic bell | ≈ 1,376 | ||
| Bouncer + X | ≈ 365 |
|
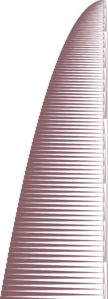
|
| Bounce-counter | ≈ 330 |
|
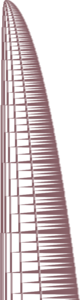
|
| Fractal | 20 |
|
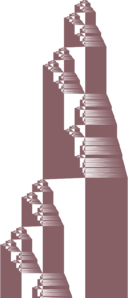
|
| Tetration counter | 19 |
|
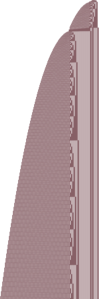
|
| Cubic bounce-counter | 13 |
|
Chaotic
| Classification | Count | Notes and Notable examples | Example space-time diagram |
|---|---|---|---|
| Irregular bell | 39 | 
| |
| Spaghetti | 26 | This is an informal description for spaghetti-code Turing machines that seem to have no predictable behavior, instead winding back and forth like a spaghetti. Any of these machines could potentially end up proven as one of the regular classifications. Indeed, many translated cyclers start their life out as spaghetti.
|

|
| Chaotic counter | 10 |
Chaotic counters have slow-growing tapes like counters, but the behavior seems to be chaotic and is as of yet unknown:
|
Records
Translated cycler preperiod
BBS(n,m) = maximum translated cycler preperiod among n-state, m-symbol TMs.
- BBS(3,2) = 101 (proven):
1RB1LB_0RC0LA_1LC0LA(bbch) (period = 24) - BBS(4,2) ≥ 119,120,230,102 (current champion):
1RB1LC_0LA1RD_0RB0LC_1LA0RD(bbch) (period = 966,716) - BBS(2,4) ≥ 293,225,660,896 (current champion):
1RB2LA0RA3LA_1LA1LB3RB1RA(bbch) (period = 483,328)
Translated cycler period
BBP(n,m) = maximum translated cycler period among n-state, m-symbol TMs.



