Counter

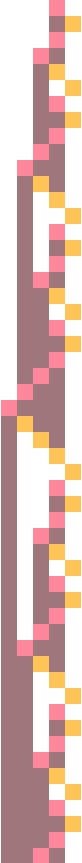
A close-up of the counter 1RB1LA_0LA0RB (bbch).

A counter is a non-halting Turing machine that, roughly speaking, has a tape that grows logarithmically with time and whose tape counts up in some sort of place-value system. Often, when the place-value system is known, we may call such counters binary counters, ternary counters, and so on.

Example

1RB1LA_0LA0RB (bbch) is a binary counter with 2 states and 2 symbols, whose spacetime diagram is shown in the image to the right. In fact, it is the only Turing machine with 2 states and symbols, up to permutations, that is a counter. In this section we give two analyses of this counter. The first analysis is coarse-grained in that it only proves non-halting and logarithmic tape growth. The second analysis is more detailed and furthermore explains the counter nature of this machine, as well as the precise step counts from one encoded number to the next.

Analysis 1

Define the macro rule R_n recursively as follows:

• R₀ = B0,
• R_n = B1 R_n−1 A0 R_n−1 A1, for n ≥ 1.

Then we find by induction, for all n ≥ 0:

• R₀: B >0 → A <0,
• R_n: B >(1n)0 → A <(1n)0,

so that, for all n ≥ 0,

A0 R_n A1: A >0(1n)0 → A <(1n+1)0.

This proves that the transcript of 1RB1LA_0LA0RB from the all zeros tape is

(A0 R_n A1)^{n ≥ 0}.

Furthermore, |R_n|, the number of steps taken by R_n, can be seen to be given by the recurrence

$|\mathbf {R} _{0}|=1,\ |\mathbf {R} _{n}|=2|\mathbf {R} _{n-1}|+3$,

which has solution $|\mathbf {R} _{n}|=2^{n+2}-3.$

Analysis 2

In this analysis, we will show that the counter indeed counts up in binary. More precisely, for a given non-negative integer n, let bin(n) denote the number n in binary. Also, let v₂(n) denote the 2-valuation of n, which is the number of times that n is divisible by 2. Then we will show:

B bin(n) >0 →[2v2(n+1) + 2] B bin(n+1) >0.

To show this, it suffices to show, for all k ≥ 0,

B 0(1k)>0 →[2k + 2] B 1(0k)>0.

The sequence B0 A1^k A0 B1^k proves this. Moreover, we can see by the spacetime diagram that B bin(1) >0 is reached (on step 1), which completes the analysis.