Bouncer: Difference between revisions
Jump to navigation
Jump to search
(→Analysis: Added number of steps) |
m (→Example: forgot head) |
||
| Line 16: | Line 16: | ||
In particular, | In particular, | ||
'''B'''<sub>n</sub>: A 0<sup>∞</sup>(10<sup>2n</sup>)0<sup>∞</sup> →[8n+8] 0<sup>∞</sup>(10<sup>2(n+1)</sup>)0<sup>∞</sup> | '''B'''<sub>n</sub>: A 0<sup>∞</sup>(10<sup>2n</sup>)>0<sup>∞</sup> →[8n+8] 0<sup>∞</sup>(10<sup>2(n+1)</sup>)>0<sup>∞</sup> | ||
thus proving by induction that the transcript of <code>1RB0LB_1LA0RA</code> on the all zeros tape is <code>('''B'''<sub>n</sub>)<sup>n≥0</sup></code>, which shows that <code>1RB0LB_1LA0RA</code> is a bouncer. Moreover, we have shown that there are 8''n'' + 8 steps between the ''n''<sup>th</sup> and the (''n''+1)<sup>st</sup> bounce. | thus proving by induction that the transcript of <code>1RB0LB_1LA0RA</code> on the all zeros tape is <code>('''B'''<sub>n</sub>)<sup>n≥0</sup></code>, which shows that <code>1RB0LB_1LA0RA</code> is a bouncer. Moreover, we have shown that there are 8''n'' + 8 steps between the ''n''<sup>th</sup> and the (''n''+1)<sup>st</sup> bounce. | ||
Revision as of 14:18, 13 November 2024
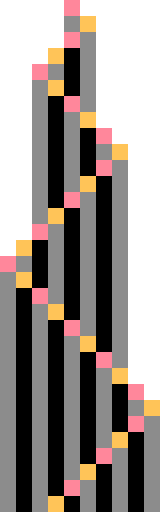
1RB0LB_1LA0RA (bbch) with 2 states, the smallest number of states for which a bouncer can appear.A bouncer is a Turing machine whose tape head, roughly speaking, alternates back and forth between the two edges of the tape in a linear fashion, growing the tape along one or both edges with each iteration. A bouncer is a possible classification of non-halting Turing machines.
Example
1RB0LB_1LA0RA (bbch) is an example of a bouncer, and its spacetime diagram is shown in the picture on the right.
Analysis
Shift rules:
B0 A1: B 10< →[2] B <01A0 B1: A >10 →[2] A 01>
Bounce rule:
Bn := A0 (B0 A1)2n+1 B0 (A0 B1)2n+2: A 00(102n)>00 →[8n+8] A (102(n+1))>
In particular,
Bn: A 0∞(102n)>0∞ →[8n+8] 0∞(102(n+1))>0∞
thus proving by induction that the transcript of 1RB0LB_1LA0RA on the all zeros tape is (Bn)n≥0, which shows that 1RB0LB_1LA0RA is a bouncer. Moreover, we have shown that there are 8n + 8 steps between the nth and the (n+1)st bounce.
See also
- Section 7 of bbchallenge's deciders write-up.